A Statistical Framework for Enhancing Basic Actuarial Assumptions Using External Data Sources and AI Techniques: Part 1

Actuarial modeling is unique in that it is driven by actuarial assumptions and not by an underlying data set. To illustrate, annual select-and-ultimate mortality rates used in actuarial modeling are constructed from industry data that is collected by the Society of Actuaries (SOA). From this industry data, mortality rates are developed and smoothed (i.e., graduated) and the resultant mortality tables are used by actuaries together with other actuarial assumptions to develop pricing, reserving, and other risk models. Actuaries do not go back to the source data that was collected by the SOA and instead work directly with the constructed mortality tables to build their actuarial models. There are several advantages with this assumption-driven approach versus a data-driven approach.

1. Actuarial assumptions form the basis for actuarial formulas and notation used in actuarial models. For example, an actuarial model to calculate individual life expectancy can be directly determined using annual mortality and survivorship rates, while a data-driven approach would be less straightforward and require the existence of a comprehensive database and several intermediate steps to do the same calculation.
2. An assumption-driven approach provides more flexibility to calculate related life expectancy measures. For example, an impaired life expectancy using actuarial modeling techniques would simply require increasing the base annual mortality rates by an impairment factor and then calculate the resultant life expectancy using the same underlying actuarial model.
3. By combining other actuarial assumptions with mortality assumptions, other interesting results can be obtained. For example, the impact of high lapse rates on the underlying mortality of a block of term insurance policies can be analyzed by combining lapse assumptions with an assumption that persisting policies exhibit higher mortality rates than lapsed policies. If morbidity rates are combined with mortality rates, a healthy life expectancy measure can be constructed that calculates the expected healthy and unhealthy life expectancy of an individual.

The richness and flexibility of this fundamental actuarial modeling technique that is assumption driven cannot be overstated. It has enabled the actuarial profession over the years to develop sophisticated and practical risk management tools to manage the complex and long-term risks facing the insurance industry. However, this established and stable modeling approach used by actuaries has its limitations in this changing world of big data, machine learning and artificial intelligence (AI). For instance, it is not clear how extraneous information from independent data sources can be incorporated to enhance base actuarial assumptions. As an example, there is no well-defined actuarial or statistical framework to recognize extraneous factors like level of income and education, or exercise and diet to modify base actuarial mortality assumptions. Some insurance companies (and actuaries) have deviated from the assumption driven approach and switched to a purely data analytics approach without a clear understanding if this new approach is actuarially rigorous and produces results that are better and implementable.   

Our Research Proposal

We propose using an assumption driven approach and complement it by developing a statistical approach to incorporate external datasets with extraneous information to enhance the base actuarial assumptions. Our approach must satisfy the following conditions:

1. It has to be statistically rigorous based on a set of reasonable assumptions.
2. It has to be built from a set of base actuarial assumptions.
3. If there are several external datasets that will be used to enhance the base actuarial assumptions, a weighting system may have to be developed in the statistical framework to recognize the relative importance of each external factor. For example, while level of income, exercise and diet may all positively impact individual mortality, in order of priority, diet and exercise may be the top two adjustments to mortality followed by income.
4. The statistical model has to provide a basis to capture the interaction effect (both positive and negative) between various adjustment factors to the base actuarial assumptions. For example, an individual who exercises regularly and follows a healthy diet should have a greater than additive adjustment factor on mortality compared to the individual adjustment factors for exercise and diet.
5. Most importantly, in constructing the statistical framework, the combined effect of these adjustment factors should be consistent, reasonable, and actuarially sound. For example, following a healthy diet may have a more beneficial mortality impact on an older versus a younger individual to reflect the greater exposure of an older individual to mortality risks generated by an unhealthy diet.
6. The statistical framework should be general enough to incorporate any relevant external datasets for enhancing a given base actuarial assumption.

Literature Review

There are a limited number of articles that discuss how to enhance a base assumption using external datasets that are not connected. The most relevant article is by Samsa G. et. al (2005). It develops a linear regression modeling technique to combine independent variables from external sources in refining the estimate of a base assumption. However, for actuarial modeling, the paper does not address the commonly faced problem on how to combine independent variables when each variable is measured at different levels.

There are more papers in the literature that identify the various factors impacting a key actuarial assumption of life expectancy and annual mortality. More specifically, diet and exercise has been recognized as indicators of life expectancy and mortality ((Daley, M. & Spinks W. (2000); Escobar, K. et. al (2020)) and the detrimental effects of smoking and alcohol consumption ((Ferrucci, L. et. al (1999); Jones, B. et.al. (2001)). However, these papers and other related research do not explicitly describe how these factors can be combined to enhance a baseline mortality assumption.

Modeling Framework

The modeling framework we have developed can be generalized to multiple risk factors each at multiple levels from various external datasets. However, for illustrative purposes, we assume we have a base actuarial assumption (e.g., annual mortality rate, incidence of disability, etc.) that we want to enhance using information from two external datasets. Suppose we have two external factors F and G with m levels for F and n levels for G. For example, F could be quality of diet at four levels—poor, average, good, and excellent. G could be level of exercise at five levels—seven days a week, five to seven days a week, three to five days a week, one to three days a week, and does not exercise. We assume the following:

1. We have estimated risk adjustment factors to the base actuarial assumption for each of the m levels of F and n levels of G;
2. we do not have any explicit interaction adjustment factors for the m times n interactions; and
3. for the m levels for factor F, we assume we have a median level m* and similarly for the n levels for factor G, we assume we have a median level n*.

Modeling Methodology: Equal Level Impact

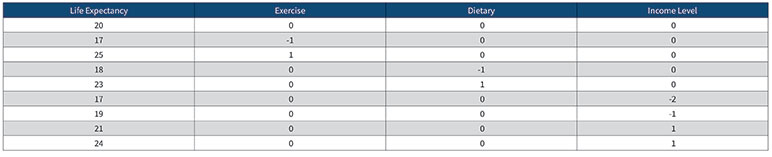
• For factor F, set level m*= 0, level m*+r = r and level m*-r = -r. In this way, all m levels will be transformed into equally spaced integers with negative integers representing levels that are below the median level and positive integers representing levels that are above the median level.
• Do the same for factor G.
• Develop a multiple regression model where the dependent variable is the adjustment factor for the base actuarial assumption, and the independent variables are the two external factors F and G with their transformed levels.
• An m by n table will be constructed with all possible combinations of transformed levels for factors F and G.
• The observed values for the dependent variable are the estimated m+n adjustment factors for a given factor with the second factor at the median level.
• The regression model is then constructed from these observed m+n values of the dependent variable and the various combinations of transformed levels of F and G.

An Illustrative Example

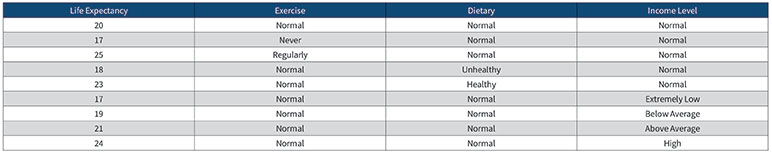
In this mortality estimate example, we will use life expectancy as a proxy for mortality rates since there is a one-to-one correspondence between the mortality adjustment factor and life expectancy. We will also assume three external factors to adjust the baseline mortality—exercise, diet, and income level.

Assume life expectancy based on a standard mortality table is 20 years.

Based on research findings from external sources:

• Life expectancy is 17 years if never exercises, 20 years if exercises at normal levels, and 25 years if exercises regularly where “normal exercise” is the median or normal level;
• life expectancy is 18 years if diet is unhealthy, 20 years if diet is normal, and 23 years if diet is healthy where “normal diet” is the median or normal level; and
• life expectancy is 17 years if income level is extremely low, 19 years if income level is below average, 20 years if income level is average, 21 years if income level is above average, 24 years if income level is high, where “average income” is the median or normal level.

We construct the data frame as follows:      

We then create the equally spaced levels from the data frame to develop the following:

We then construct a multiple linear regression model as follows:

Based on the above numerically transformed levels example, the following is the regression model:

Now we can calculate the adjusted life expectancy for any level combinations of the three external factors—diet, exercise, and income.

For example, someone who has a healthy diet, normal exercise level and below average income would have an estimated life expectancy calculated as:

20.65+4*0+2.5*1+1.81*(-1) = 21.34

Note

1. If the various factor levels show a consistent increasing or decreasing impact on the baseline actuarial assumption that is estimated, then the corresponding interaction factors from the regression model will show a logical pattern as well. For example, an individual with a healthy diet who exercises regularly should show a greater increase in the baseline life expectancy than another individual with a healthy diet who never exercises. Furthermore, an individual with an unhealthy diet who never exercises will show a predicted life expectancy that is lower than a similar individual with a healthy diet who never exercises.
2. The equal level impact modeling approach we have developed satisfies all the six conditions we have stipulated for an acceptable modeling framework to estimate the interaction impact of various external factors.

Impact of Our Research

Our research solves the fundamental dilemma facing our actuarial profession on how to evolve and transform itself in the advent of access to various external sources of data and new modeling techniques. The solution is more than involving statisticians and data scientists in actuarial modeling since actuarial modeling is unique and as mentioned in the introduction to this paper, is assumption-driven and not data-driven. The biggest contribution of this research is that we have developed a general statistical approach on how to combine independent sources of information on various factors impacting a base actuarial assumption in a logical and consistent manner while still preserving the basic assumption-driven methodology used by actuaries. This research has far-reaching implications of how actuarial modeling could be transformed in the future. In virtually all forms of actuarial modeling, we do not have a complete database of information that could impact a given actuarial assumption. But as demonstrated in our examples, we may have information on specific factors at various levels impacting a base actuarial assumption without any accompanying data, or from independent, unconnected data sets. Our research demonstrates a statistically rigorous and actuarially sound approach to capture these various relevant external data sets to adjust the base actuarial assumptions.

Statements of fact and opinions expressed herein are those of the individual authors and are not necessarily those of the Society of Actuaries, the newsletter editors, or the respective authors’ employers.