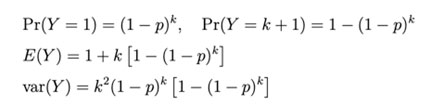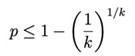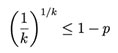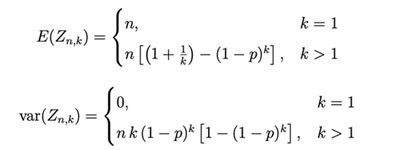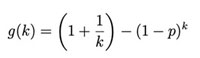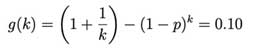The Probability Principle of Group Testing: The Full-Scale Nucleic Acid Testing in Tianjin

This article was originally published on the WeChat account of the China Association of Actuaries on January 19, 2022. The link is as follows: https://mp.weixin.qq.com/s/3Ko0p7jTNFnb-89b-VIuMw.

Beginning at 7 a.m. on Jan. 9, 2022, nucleic acid testing for COVID-19 began for all people in Tianjin, including the Jinan, Nankai, Dongli and Xiqing districts. Testing began in the 12 remaining districts the following day. The group testing method was used, with 10 people in each group. By noon on Jan. 11, the first round of testing had sampled 11,912,280 people, and the results of 7,892,591 were published, with 77 positive cases. Together with previously reported positive infections, it was a total of 97 cases.[1] By 2 p.m. on Jan. 12, the first round of full testing had sampled a total of 12,523,310 people, still with 77 positive cases. Together with the previously reported positive infections, the total number of cases was 137.[2] Testing continued throughout all districts and on Jan. 19, Tianjin held its 173rd press conference on the prevention and control of the spread of pandemic. It reported that as of midnight on Jan. 18, Tianjin had 326 confirmed cases of the current round of indigenous new coronavirus pneumonia.

Group testing has greatly reduced testing time and improved testing efficiency. A brief introduction to the principle of group testing is given here, and the efficiency of such testing is analyzed, particularly from the perspective of probability theory.

The Concept of Group Testing

The concept of group testing has been around for a long time, and the method has been used for over a decade to ensure the safety of donated blood. Blood banks test donations to ensure they are free of HIV, hepatitis viruses, and so on. As the name implies, group testing involves taking a portion of blood from multiple people and pooling that blood into one group sample. Some blood from each person in the group is also kept in case retesting is required. Virus testing (usually nucleic-acid based) is performed on the pooled samples. If the test is negative, it indicates that all individual samples are negative. If the test is positive, it indicates that one or more samples are positive, at which point a second round of testing is performed on each of the retained samples to find out which individuals are infected.

For example, imagine that 50 samples need to be tested. If they are tested one by one, then 50 tests are required. However, if the samples are divided into 10 groups of five and each is pooled, only 10 tests are required in the first round of testing. If four groups in this round are positive, then 20 tests (one for each of the five people in those groups) are performed in the second round. The total number of tests will be 30.

In August 2020, the U.S. Food and Drug Administration released regulatory requirements for group testing in the detection of COVID-19 outbreaks in the United States.[3] Wicklin has discussed the efficiency of applying group testing in the this context.[4]

Intuitively, group testing only makes sense when the probability of each sample being infected is small.

The Probability Principle of Group Testing

Let there be k samples within a group. If they are tested one by one, it is necessary to test k times. With group testing, two results will occur: when the confluent samples are negative, the testing ends, and the number of tests is 1. When the confluent samples are positive, they are tested individually k times, and the final number of tests is 1 + k. The number of tests for group testing is denoted by Y, which is a random variable. Let the probability of each sample being infected be p, 0 < p < 1.

Regarding the variable Y, the following conclusions are drawn.

Conclusion 1. The probability distribution, expectation and variance of Y are as follows:

The most direct purpose of group testing is to reduce the number of tests, which makes E(Y) < k hold, then the inequality between p and k is obtained.

Conclusion 2. For a given k, the p required by group testing satisfies the following condition:

Correspondingly, for a given p, the k required for group testing satisfies the following condition:

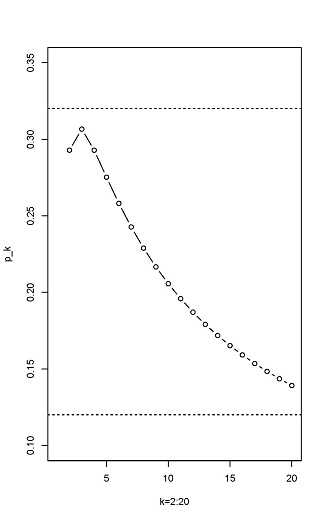
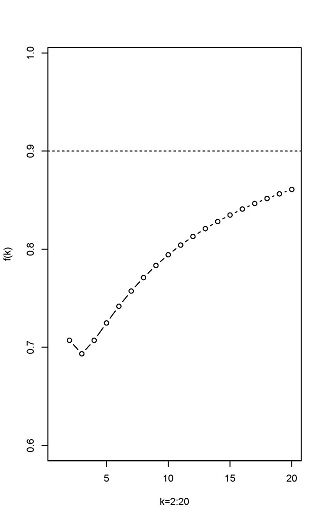
These two conditions are illustrated in Figure 1. The left panel gives an upper bound on p for a given k. Group testing is meaningful when the actual p is less than this upper bound. It can be seen that, due to the low rate of positive Omicron infections (on the order of 1 in 100,000 from Tianjin and 1 in 10,000 from Jinan), group testing is feasible even for larger k (e.g., k = 20).

Figure 1
The Relation Between p and k

The right panel illustrates the same thing from the other side. The vertical coordinate f(k) is (1/k)^1/k. The group testing scheme is feasible even for an infection rate of p = 0.1 and k = 20. Also, for a given p, no matter how small it is, k cannot be arbitrarily large. Mathematically, it is .

Now suppose there are n persons, and n is a multiple of k. Divide the n individuals equally into n/k groups and perform group testing. If Y denotes the number of tests in group i, then the total number of tests is Z_n,k = Y₁  + Y₂ + ... + Y_n/k .The random variable Z_n,k  gives the following conclusion.

Conclusion 3. The expectation and variance of the variable Z_n,k  are as follows:

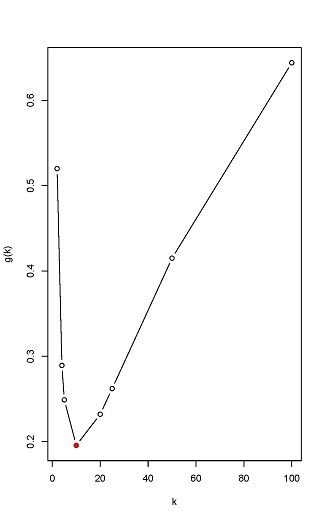
In the following, only the expectation of the variable Z_n,k  is considered. The problem boils down to considering the optimal k for the given n and p such that the expectation of Z_n,k  is minimized. It ultimately means solving the function g(k) with respect to k as a minimal value, which can be viewed as a ratio with respect to the total number of tests n corresponding to a one-by-one test scheme. The smaller the ratio, the better.

The optimal value of k can be obtained by solving it numerically.

Example 1. Solve for the optimal value of k under the following parameters (n, p). Only when n is divisible by a k is that k considered.

(1) n = 100, p = 0.01
(2) n = 1,000, p = 0.05
(3) n = 1,000, p = 0.001

Using R software, the following conclusions were obtained.

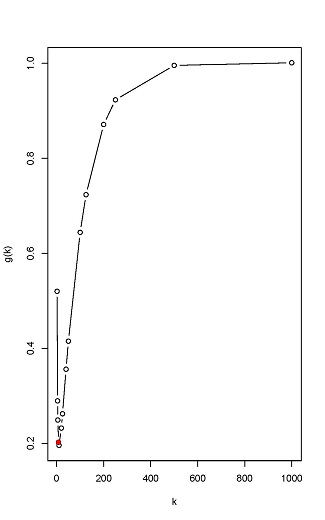
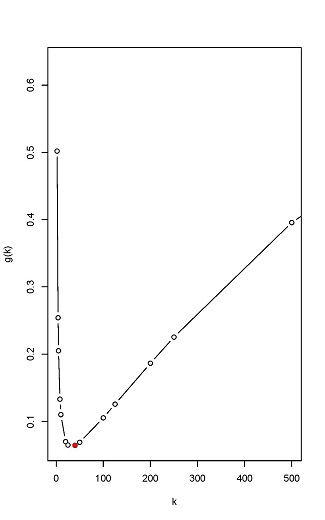
(1) k = 10, g(10) = 0.1956.

The ratio here is close to 0.20, which means the efficiency is 5 times higher than that of the one-by-one test scheme. It can be verified that the same conclusion is obtained when n = 1,000, at which point the number of available values of k is higher. However, the number of people in each group is not too large (e.g., greater than 50) in practice. Essentially, the optimal k is the same.

(2) k = 5, g(5) = 0.4262.

Note that the ratio here is still large, mainly because p, the probability of a positive result, is relatively large, equaling 0.05.

(3) k = 40, g(40) = 0.06423.

At first glance, k = 40 is a bit large, and it can be verified that 1 – (1/40)^1/40 = 0.088, which is much larger than the p = 0.001 given here. However, referring back to Figure 1, this grouping is feasible.

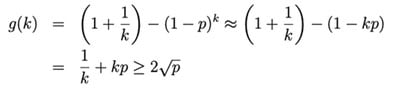
Note that if p is very small (e.g., 1 in 10,000) in the actual problem, then g(k) has the following approximation:

From the last inequality above, the optimal k approximation is obtained by

The optimal group testing for the three cases in Example 1 is given in Figure 2.

Figure 2
The Choice of k in Group Testing

Example 2. Combined with the detection results in Tianjin, if p = 1/10,000 and k = 10, then the ratio g(k) is:

After calculation, the theoretically optimal k can be chosen as 100, and the corresponding g(k) = 0.02.

Conclusion

When the vast majority of people tested are healthy, the probability of a positive in the population will be small. When the probability of positive results is extremely small, group testing can be very effective. If the testing process is highly sensitive, it is theoretically possible to pool dozens of samples and thus test a larger number of people quickly.

This article shows that when testing a large number of samples, group testing can be used to reduce the number of tests required. Combined with the effectiveness of current domestic controls, the number of tests could theoretically be reduced to 2 percent by group testing 100 people at a time if a 1 in 10,000 infection rate assumption were used. The current method of testing 10 people per group is conservative enough.

Finally, it should be noted that this article is about the probabilistic principal approximation of group testing. For convenience, the effect of randomness is not analyzed further, and the problems faced in practice, such as whether conflating many samples would dilute the concentration of the virus and thus affect the sensitivity of the assay, are not considered.

Statements of fact and opinions expressed herein are those of the individual author and are not necessarily those of the Society of Actuaries, the editors, or the respective author’s employer.