An Exploration of the Quantum Actuary

Quantum mechanics is an important concept in modern physics, which was proposed by Max Planck in 1900. He found that radiant energy is discontinuous and can only be taken as an integral multiple of the unit of energy. Later research shows that not only does energy show this discontinuous separation property, but other physical quantities such as angular momentum, spin, and charge also show this discontinuous quantization phenomenon, which is fundamentally different from classical physics represented by Newtonian mechanics. If a physical quantity has the smallest unit and cannot be separated continuously, it can be said that the physical quantity is quantized, and the smallest basic unit is called quantum. Many phenomena in nature and society show the characteristics of “quantization,” of course including the insurance market.

Probability is the cornerstone in the actuarial calculation while the quantum mechanics could give different perspectives on the probability. Just like force, mass, acceleration, energy, and momentum in classical mechanics are continuous deterministic variables, actuarial variables, such as premium, claim, profit, expense, and distribution earning, are also considered to be continuous deterministic variables. In quantum theory, when several particles interact with each other, due to the properties of each particle having been integrated into a whole property, it is impossible to describe the properties of each particle alone, but only the properties of the whole system, which is called quantum entanglement. In the insurance field, there also exists the phenomenon of quantum entanglement. The reason why insurance can be priced and provide risk protection is not based on the individual risk probability, but the overall risk probability. In the face of a complex and changeable quantized insurance market, traditional actuarial theory may lack effective explanatory and predictive power. Each policy can be regarded as the smallest unit and cannot be separated continuously, so it can be said that each policy is similar as the quantum and have the quantum property. In this article, we start from a new approach to explore the quantum application to the insurance market by using some simple Hamiltonian operators. By solving the corresponding partial differential equation, insurance phenomena could be quantitatively described under the new framework of quantum actuarial theory.

The Quantum Theory

The Schrödinger equation governs the wave function of a quantum-mechanical system that is a key result in quantum mechanics and its discovery was a notable turning point in the applied sciences. The equation expression using the bra and ket notation is given by[1]:

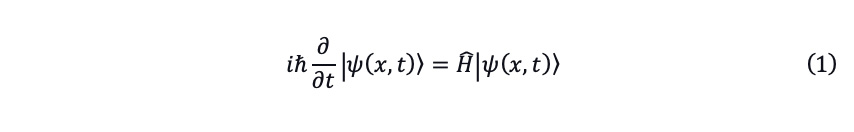
where i is the imaginary unit, ℏ is the reduced Planck constant, ψ(x,t) is the wave function with the position x and time t , Ĥ is the Hamiltonian operator.

A special case of this equation that admits a statement in those terms is the position-space Schrödinger equation for a single nonrelativistic particle of the one dimension given as[1]:

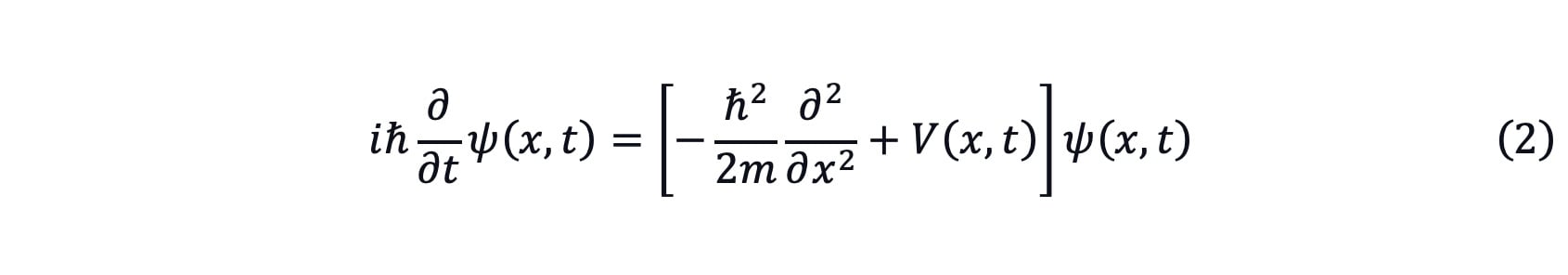
where m is the mass of the particle and V(x,t) is the potential that represents the environment in which the particle exists.

In the physical world, |ψ(x,t)|² is regarded as the probability of a particle arriving at position x at time t and ∫|ψ(x,t)|²=1 which was first proposed by M. Born.

These equations govern the dynamics of quantum mechanics, quantum field theory, wave-particle duality applicable in several physical phenomena.

Suppose that the time evolution function can be separated from the ψ(x,t) which means ψ(x,t)=ψ(x)f(t). Substitute this expression into equation (1).

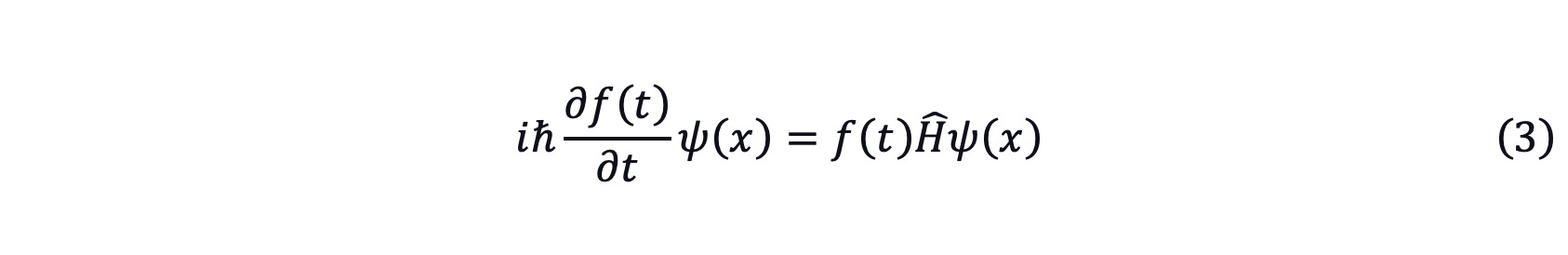
divided by ψ(x)f(t)

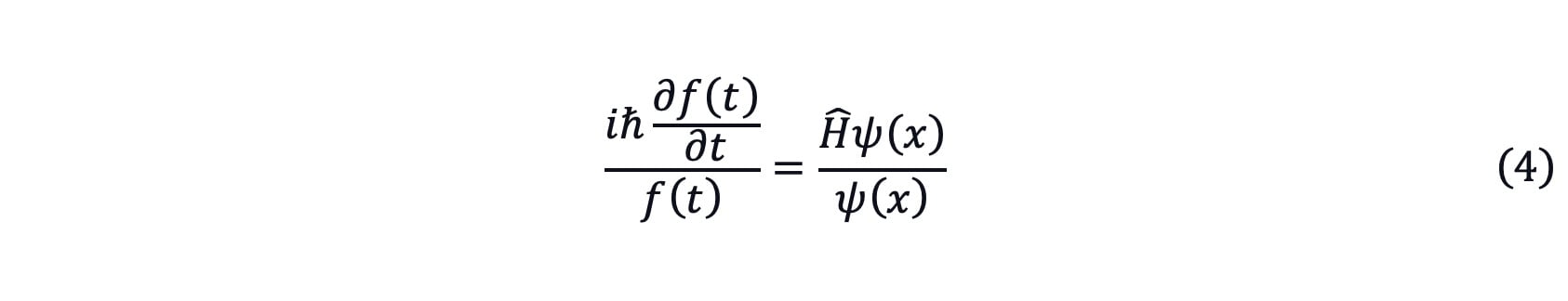
The left part is the only function of t and the right part is the only function of x. So, this equation holds only when it is constant. Take this constant as E.

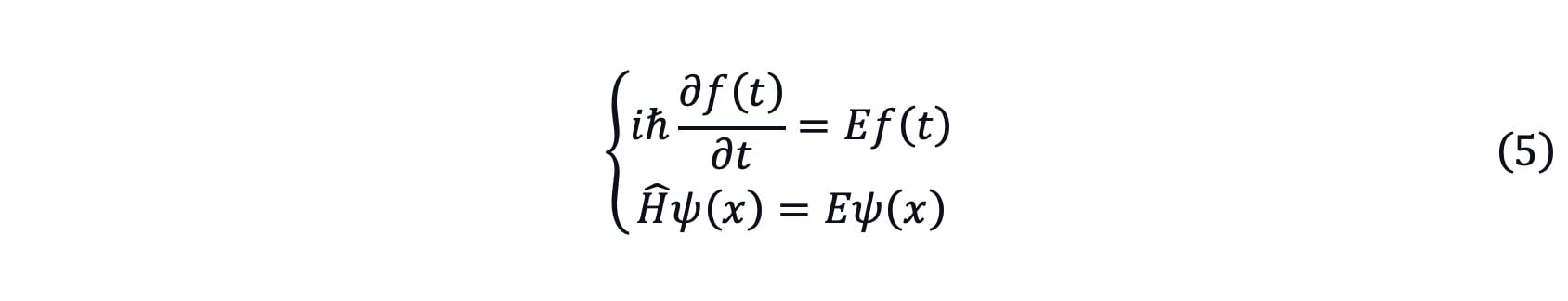
By solving the first equation of equation (5), the time evolution function can be written as[2]

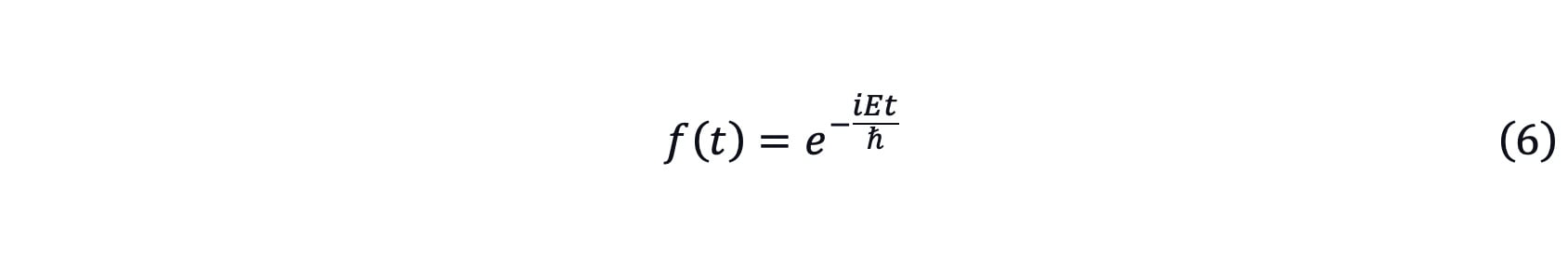
By solving the second equation of equation (5), ψ(x) can be regarded as the eigenfunction of the Hamiltonian operator Ĥ and E can be regarded as the eigenvalue.

In the actuarial world, ψ(x,t) could be extended to the probability amplitude of claim, profit, premium, distribution earning, and so on. Suppose ψ(x,t) satisfies the position-space Schrödinger equation which is equation (2). m could be regarded as certain constant for typical insurance while V(x) could be introduced into theory to describe the influence of external environment on insurance market. The constant of m or ℏ could be derived by experience study for the insurance market. However, the Hamiltonian operator Ĥ is hard to define in the insurance market. In the next part, some simple Hamiltonian operators would be used to show how these theories are used in the insurance market.

Simple Application

Infinite Square Potential Well

Take the easiest example at first which is called infinite square potential well. Let ψ(x) be the profit probability amplitude of a certain insurance product. Next, we consider the boundary condition of the ψ(x). The insurance product often has the sum assured which is the maximum claim amount during the coverage period. Meanwhile, insurance is a strongly regulated industry. Different countries have various solvency requirements. Considering these two factors, the profit probability amplitude ψ(x) has the bottom boundary –a which means ψ(x)=0 when x≤-a. On the other hand, ψ(x) also has the upper limit. The maximum profit for an insurance product is the accumulated premium without any claim. Meanwhile, the premium rate for a product can’t be infinite. As mentioned before, insurance is a strongly regulated industry. Therefore, the pricing for the premium rate for insurance product is restricted by regulators. On the other hand, the insurance market is a competitive market, so an abnormally high premium rate would be priced out of the market very soon.

So, the profit probability amplitude ψ(x) has the upper boundary b which means ψ(x)=0 when x≥b. After the transformation of the coordinate,

ψ(x') can only be exited when |x'|≤c, where The next difficult part is to define the external environment function V(x). The environment for the insurance market is very complex. The profit for the insurance product is affected by the incidence rate, medical cost, inflation, regulatory policy, competitors, the development of medical treatment and so many factors. Let’s suppose some simple expressions for V(x).

If the V(x)=0 when |x|≤c, the ψ(x) can be derived as following by using equation (5).

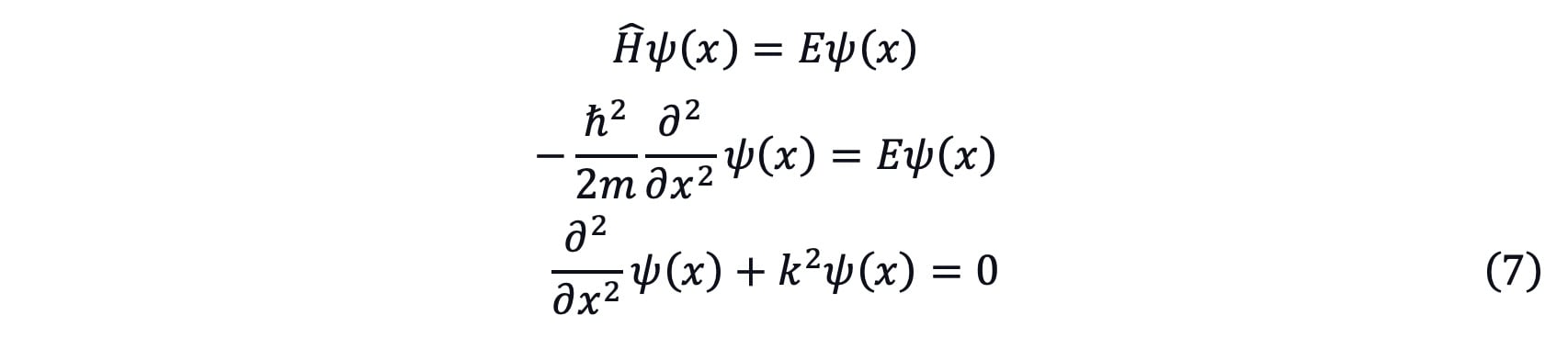
where 

By solving the partial differential equation, the particular solution for equation (7) can be written as

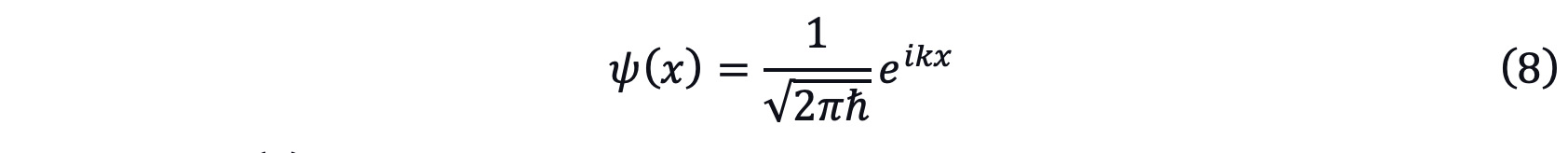
Moreover, ψ(x) should be satisfied by the boundary condition which is

ψ(c)=ψ(-c)=0               (9)

ψ(x) should satisfy the normalization condition which is

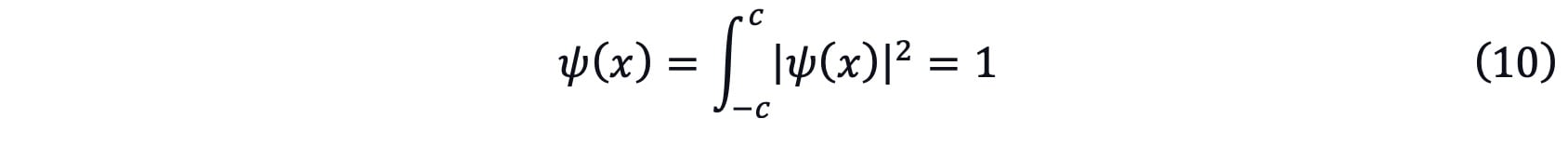
Considering equations (8), (9), and (10), we can finally get an even parity expression as[3]

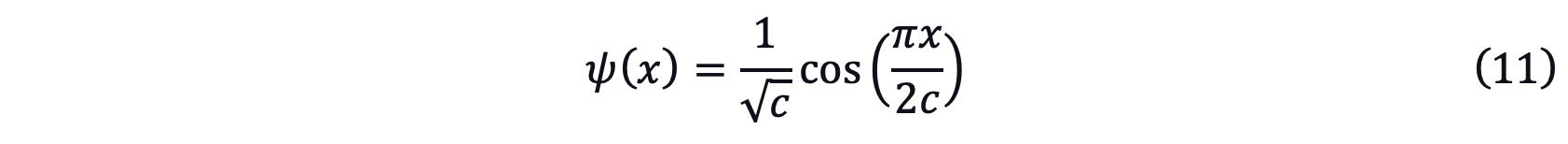
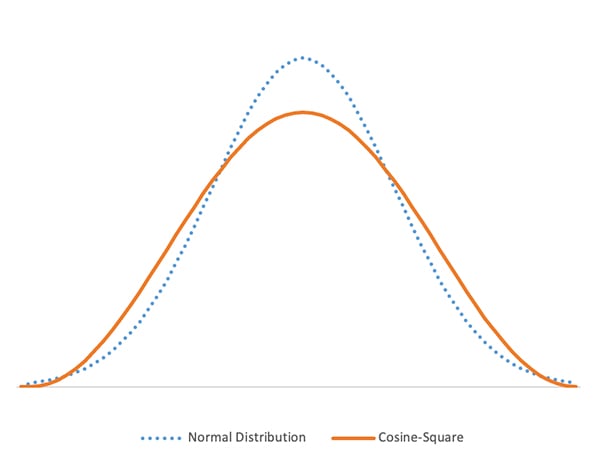
The probability density function |ψ(x)|² is cosine-square function in this case. According to the central limit theorem, almost any set of independent and randomly generated variables could be described as normal distribution. As shown in Figure 1, cosine-square function has the similar shape as the normal distribution. Although cosine-square function doesn’t have a fat tail and sharp peak, it is a good approximation for normal distribution.

Figure 1 |ψ(x,t)|² for Infinite Square Potential Well

Let’s see another application in this infinite square potential well. If V(x) suddenly disappears in |x|≤c, which means the external environment suddenly changed, the probability function of the derivative of could be written as

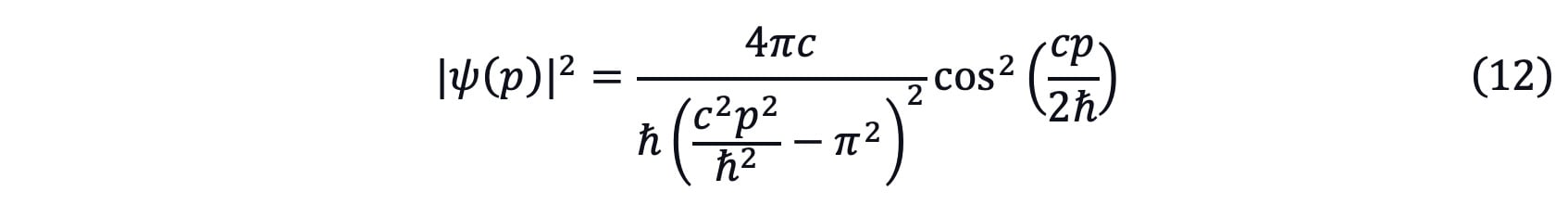
This formula could mean the probability of the change rate of profit when the external environment, such as the restriction of regulators, suddenly changed in the quantum theory of this case.

Potential Barrier Penetration

For this example, we try to use quantum mechanics to calculate the probability that a substandard insured passes or fails an underwriting examination under the potential barrier penetration. Let’s assume ψ(x) is the sum assured probability amplitude of certain insurance products this time with the minimum amount a. An insurance product often has the requirement of physical examination. V(x) could be introduced to simulate this requirement to some extent as the following expression.

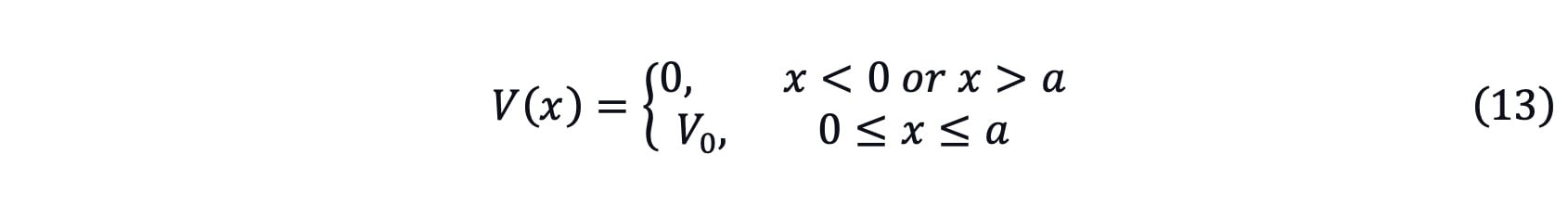
It is assumed the physical condition of a certain insured could be quantified as E. If this insured wants to purchase the insurance product with the sum assured above a, he/she should cross the barrier between 0≤x≤a.

Figure 2 V(x) for Potential Barrier Penetration

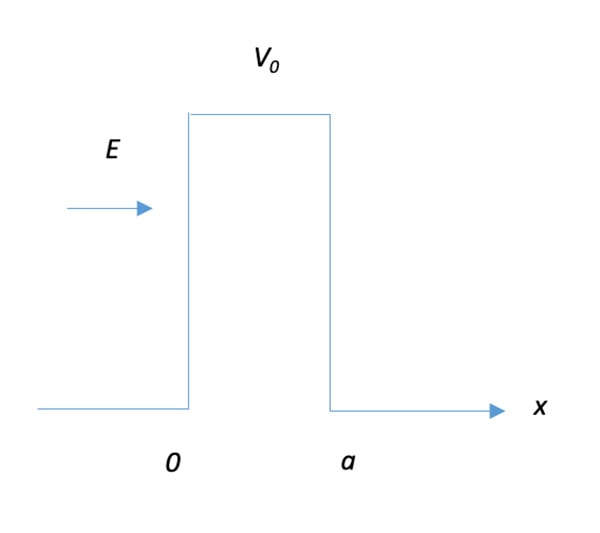
For the standard insureds which means E≥V₀, they could obviously pass the barrier. For the substandard insureds which means E<V₀, the situation is quite different in the classical world and quantum world. In the classical world, if E<V₀, ψ(x) can’t cross the barrier and would be catapulted at x=0. However, in the quantum world, ψ(x) could cross the barrier with certain probabilities. It is also uncertain whether a substandard insured could pass the underwriting examination in the realistic insurance market. It depends on the professionalism of the examination institutions and equipment, the physical condition of the insured on the examination date, the importance and contribution of the insureds to the insurance company and so many other factors. Moreover, the insurance company could accept the substandard insured by charging extra premiums or adding the exclusions even the substandard insured’s physical condition doesn’t meet the requirement. So that the quantum world’s phenomenon is closer to the realistic insurance market.

If E<V₀, the Schrödinger equation could be written as

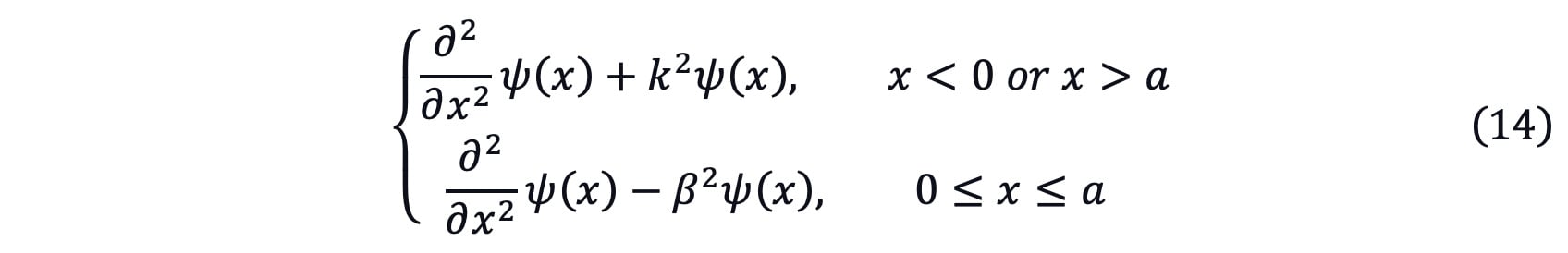
where

ψ(x) could be written as[4]

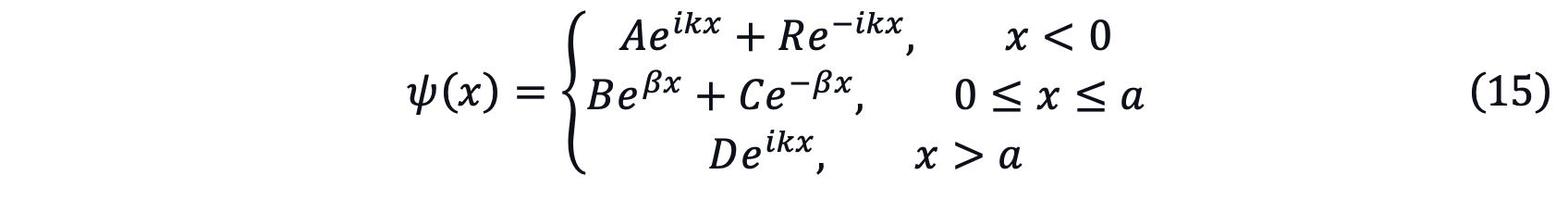
ψ(x), ψ'(x) should be continuous at boundary.

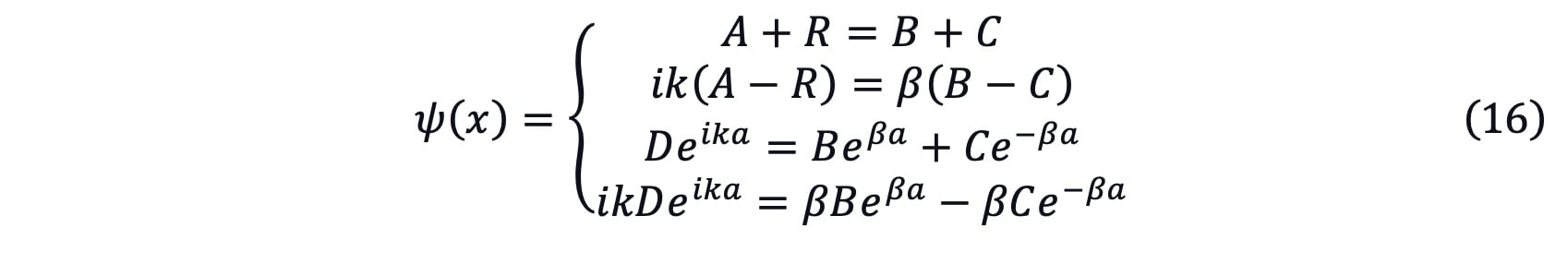
Then we could get the penetration coefficient and reflection coefficient

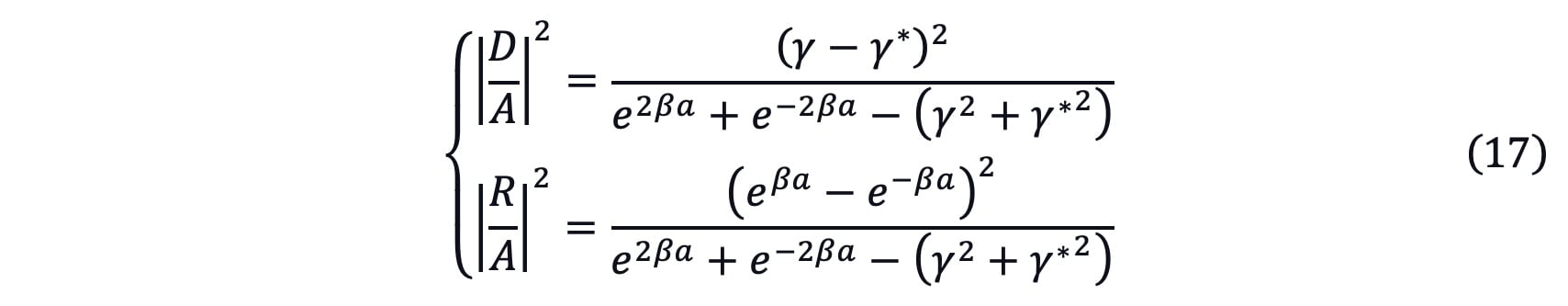
where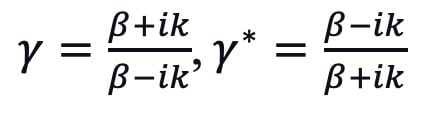

In this case, the penetration coefficient could be used to describe the probability that an insured passes the physical examination while could be used to describe the probability that an insured fails the physical examination

It can easily be proven that

When In this simplified formula, the penetration coefficient is a negative exponential decay function depends on the sum assured a, physical examination requirement V₀ and insured’s physical condition E. When the deviation between E and V₀ is greater, the probability of substandard insureds passing the physical examination decreases significantly. This probability may be useful to get the accurate incidence rate for the insurance products by considering the standard insurers and partial substandard insurers together.

Harmonic Oscillator

Harmonic vibration is a very common phenomenon in the classical physical word. It can be simply summarized as the reciprocating motion near the equilibrium point. In the insurance market, we can assume the external environment as two types of information that appear periodically which are close to the harmonic vibration to some extent. If the influence of the external environment is considered to be similar to a simple harmonic vibration, the V(x) could be written as the following

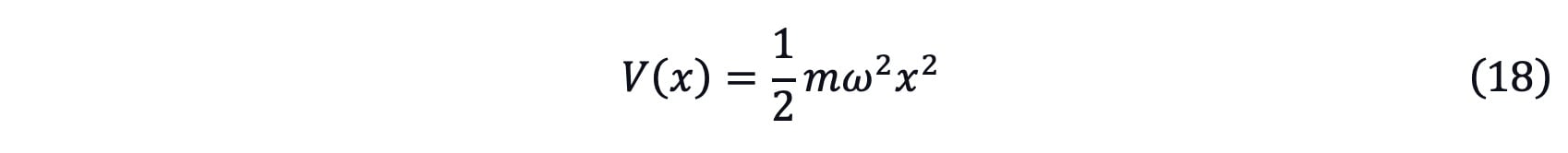
By using the Schrödinger equation as equation (5)

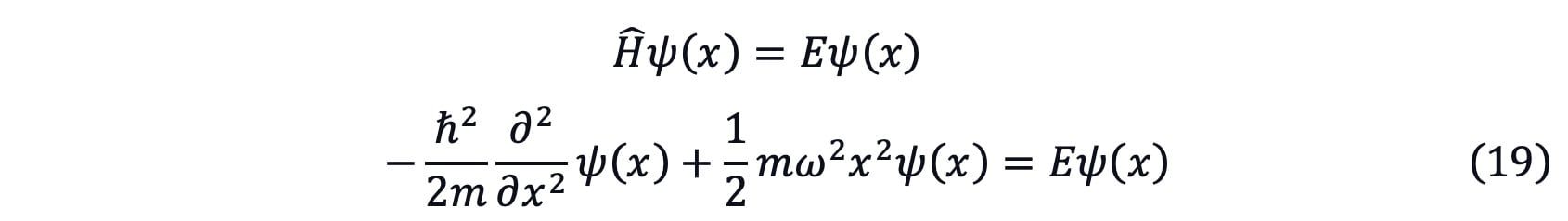
Let 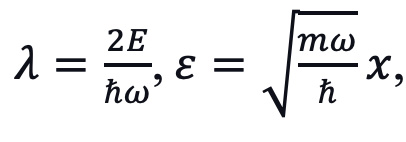then equation (19) could be written as

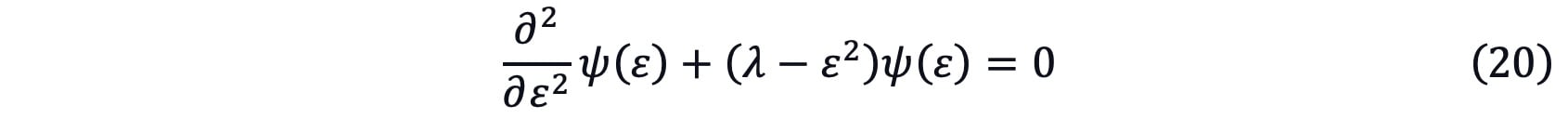
By solving the partial differential equation, the particular solution for equation (20) can be written as[5]

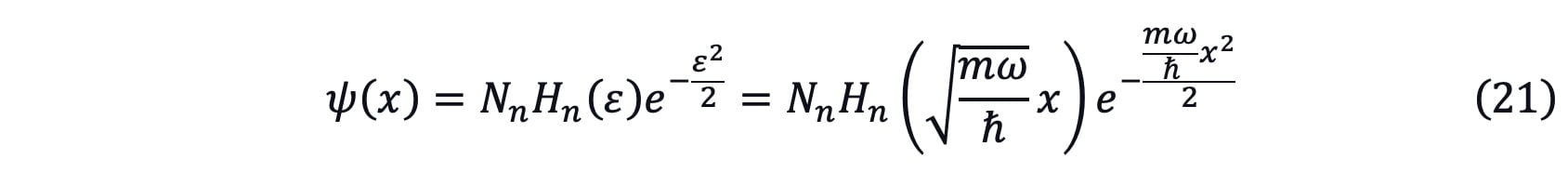
where

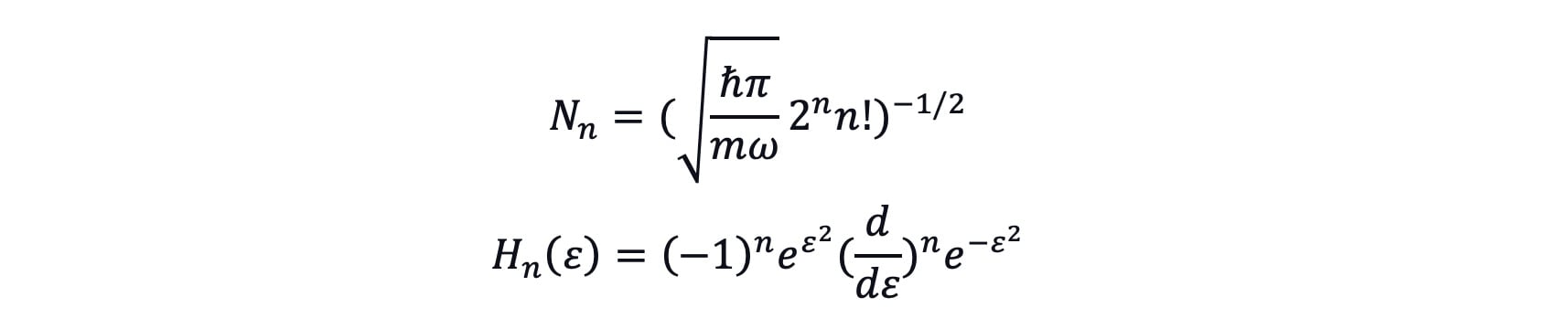
If take n=0, then

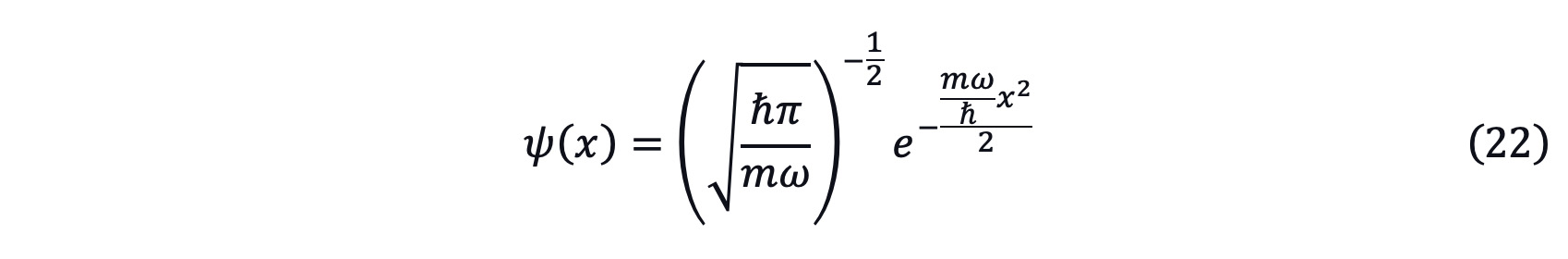
The expression for ψ(x)² is known as the normal distribution when n=0. According to the central limit theorem, almost any set of independent and randomly generated variables could be described as normal distribution. When n>0, ψ(x)² is composed of several Gaussian wave packets. In this case, ψ(x)² could be used to explain the claim, profit or distribution earnings as long as the external environment is more like a harmonic vibration. Take the claim incidence rate as an example, each insurance liability for the insurance product has the best estimation assumption. The actual claim incidence rate could be regarded as reciprocating fluctuation near the best estimation assumption which is similar as the harmonic vibration. Then equation (22) could be used to simulate the deviation between the actual incidence rate and the best estimation assumption. This can be easily to promote to other assumptions like lapse, expense, investment rate and so on which may be useful in the actuarial experience study work.

Conclusion

In this article, we start from introducing the quantum probability |ψ(x,t)|² and compare it in the actuarial field. By constructing several simple Hamiltonian operators, several examples are explored in the insurance market by solving the corresponding partial differential equation of the Schrödinger equation. The probability function |ψ(x)|² is quantitatively described and discussed in the infinite square potential well, potential barrier penetration and harmonic oscillator. For further research with more complex Hamiltonian operators in the insurance market, the probability density function |ψ(x)|² may not have the closed-form solution. Dirac notation and Matrix notation would be used, which is the foundation in quantum computing.

Statements of fact and opinions expressed herein are those of the individual authors and are not necessarily those of the Society of Actuaries, the newsletter editors, or the respective authors’ employers.