Quantum Actuary:Reshaping Insurance Cognition

Physics is the natural science that studies the most basic structure, common interactions, and general laws of motion by using experimental and thinking methods in the material world. To generate the general laws of any phenomenon in the real world, we often establish relevant theoretical assumptions and methods supported by extensive experiments. We can derive from these theories and models not only to acquire the objective laws of historical occurrence but also to have a chance to predict a glimpse of the future.
Quantum physics is an important theory in modern physics that describes the motion and interaction of particles in the microscopic world. Quantum physics has many advantages. It can describe and explain peculiar phenomena in the microscopic world, such as quantum superposition states, quantum entanglement, and quantum tunneling. These phenomena cannot be explained in classical physics. For example, quantum superposition states refer to a particle being able to be in multiple states at the same time, where these states are superimposed on each other, rather than being in only one deterministic state, as in classical physics. The characteristics of this superposition state are widely used in quantum computing and quantum communication.
Quantum actuary, as a new field of exploration, is trying to apply quantum physics to the insurance market, which is different from the traditional actuarial theory. Quantum physics has been widely applied in many fields, such as quantum computing, quantum communication, quantum chemistry, quantum cognition, and quantum economics. Many phenomena in nature and society show the characteristics of "quantization," of course including the insurance market. With the advancement of technology and socio-economic development, the insurance industry is also facing new situations and demands. This article will mainly explore the quantum characteristics in some insurance phenomena. By using the quantum theory, this article will aim to revolutionize traditional insurance thinking, reshape the insurance cognition, and explore the new paths for modern actuarial science.
Why use quantum physics in insurance but not other physics?
Before answering this question, let’s show the main characteristics of quantum physics compared with classical physics.
- Quantization: If a physical quantity is in the smallest unit possible and cannot be separated continuously, it can be said that the physical quantity is quantized, and the smallest basic unit is called quantum. In classical physics, there is no limit to the minimum value of any physical quantity change, and it can undergo any continuous change. In quantum physics, physical quantities can only be changed one by one in a certain basic unit. For example, in classical physics, energy is continuous and can take any value. In quantum physics, however, energy levels are quantized, meaning they can only have certain discrete values. This is particularly evident in the behavior of electrons in atoms and molecules, where they can only exist in specific energy levels or orbitals.
- Quantum Superposition: Quantum particles can exist in a superposition of multiple states simultaneously. This means that until measured, a particle can be in a combination of different states, rather than being in a definite state like classical objects. This property is often exemplified by Schrödinger's famous thought experiment involving a cat that is both alive and dead until observed.
- Wave Particle Duality: Wave particle duality states that particles, like electrons and photons, can exhibit both wave-like and particle-like behaviors. On one hand, particles exhibit properties such as mass, charge, and discrete energy levels. On the other hand, they can also exhibit wave-like behavior, such as interference and diffraction. Wave-particle duality challenges our classical understanding of particles as exclusively discrete objects. Instead, it suggests that particles can exist as both particles and waves, depending on how they are observed or measured.
- Heisenberg Uncertainty Principle: The Heisenberg Uncertainty Principle is a fundamental concept in quantum physics that states there is a natural limit of precision for the measurement (observation) of certain pairs of physical properties on any matters, which known as complementary variables (or what we call quantum pairs), such as position (x) and its momentum (p). The more accurately one property is measured, the less accurately the other can be measured. This intrinsic uncertainty is a consequence of the wave-like nature of particles.
After understanding the main characteristics of quantum physics, let's explore its compatibility with the insurance market.
Actuarial Particle
The insurance market consists of plenty of insurance companies. Insurance companies create and manage numerous individual or group policies, each tailored to the specific needs and circumstances of the policyholder. An insurance policy is a legal agreement between an individual or entity (the policyholder) and an insurance company. The policy specifies the coverage limits, premiums, deductibles, and other important details. It outlines the terms and conditions of coverage for a specific type of risk, such as life, health, or accident. Each policy or each insured can only have certain discrete values no matter corresponding claim, premium, or cash value specified in the terms and cannot be further divided, which is consistent with quantization characteristics in quantum physics.
Combined with quantum theory, the smallest unit in the insurance market could be each policy or each insured according to different evaluation indexes, which could be defined as “actuarial particle.” These actuarial particles are the fundamental building blocks of the insurance market. The concept of actuarial particle reveals the quantization of the insurance market, which is one of the prerequisites for applying quantum physics to the insurance market and it is the main reason why the insurance market can exhibit quantum characteristics.
Schrödinger's Insured
As mentioned above, the insured can be regarded as the smallest and indivisible basic unit, which is in line with the characteristics of quantization. Therefore, the uncertainty of the risk state of the insured can be regarded as the quantum superposition state of the actuarial particle in the insurance market. Combined with quantum theory, the insured, as an actuarial particle in the insurance market, has a certain initial value. It has been in the superposition state of survival and death during the insurance period until the triggering event. In the insurance market, this concept will overturn traditional insurance cognition and pose interesting implications, as insureds constantly dwell in a state of uncertainty, oscillating between survival and death, until a triggering event occurs.
Combined with insurance practice, insurance companies often need to observe the state of the insured through underwriting when issuing policies to confirm whether the actuarial particle meets the basic conditions for entering the insurance risk pool. Through health notification, the insured's risk profile is initially evaluated and recorded at the time of policy issuance. Multiple factors such as age, health, occupation, and lifestyle contribute to this risk assessment process. Therefore, the risk status of the insured is a certain state when the policy is issued, which means there exists a certain initial value for each actuarial particle in the concept of physics. After the policy takes effect, because the insurance company stops observing the risk status of the insured, the insured's risk status has always been uncertain for the insurance company. It means that the insured's state can be in a quantum superposition of survival and death, each with a corresponding quantum probability. The quantum superposition state of this actuarial particle will continue consistently until the insurer re-examins the risk state of the insured or there is a filing of a claim by the policyholder, which could be called the triggering event. When this moment arrives, the individual's state of superposition ceases to exist as their fate is determined, and then collapses into a certain risk state. If the event doesn't occur, the insured individual continues to reside in the superposition, perpetually uncertain of their future. So, for insurance companies, we can define the insured as “Schrödinger's insured” which is similar to the “Schrödinger's cat.”
The concept of quantum superposition introduces unique challenges and opportunities within the insurance market. On one hand, insurers may find it challenging to accurately assess risks and probabilities associated with policies by using traditional actuarial theory due to the inherent uncertainty presented by quantum superposition. However, this concept also opens up possibilities for innovation of insurance pricing and valuation. Based on the quantum probabilities of each superposition state, selecting an appropriate quantum wave function model for data analysis and prediction can enable insurance companies to better evaluate and understand the likelihood of various risks occurring. As technology advances and our understanding of quantum physics deepens, the realm of quantum superposition in insurance promises exciting prospects for a more adaptable and accurate risk assessment.
Wave-particle Duality in Insurance
Just as particles can exhibit both particle-like and wave-like behavior, insurance markets often experience a similar duality. Let’s delve into the intriguing hypothesis that the insurance market can be likened to have wave property, while actuarial particles can be represented as discrete particles. Let us explore this paradoxical concept to gain a fresh perspective on the insurance industry.
Firstly, the insurance market could be regarded as having wave behavior characteristics. In the macroscopic view, the insurance market fluctuates and evolves over time, so it can be perceived to have wave property due to its collective behavior of abundant actuarial particles. It is influenced by a plethora of interconnected factors such as regulations, economic environments, medical development and insured’s behavior. This constant ebb and flow reflects the wave-like property of the insurance market. The wave property of the insurance market can be observed through various phenomena. Insurance premiums tend to rise and fall in cycles, known as underwriting cycles. In periods of economic boom, insurers are willing to underwrite risks more liberally, leading to increased competition and lower premiums. Conversely, during economic downturns or after a large-scale catastrophe, premiums rise as insurers reassess their risk appetite. This cyclic behavior demonstrates the wave-like tendencies of the market.
Just as waves interact and interfere with each other, risks within the insurance market are intertwined in complex ways. Interference means that when two or more waves meet and superimpose at the same time, they will overlap or cancel each other to produce new wave patterns. This situation also exists in the insurance market. For example, multiple insurance companies launch different products to the market at the same time, which will lead to the diversity of insurance products and price competition. Different companies may launch products with similar product design forms, but their prices, coverages and service qualities may have huge differences. When consumers choose insurance products, they need to consider the differences between different companies, conduct comprehensive comparison and evaluation, and finally choose the most appropriate insurance product. This process of competition and choice is the embodiment of interference in the insurance market. Diffraction refers to the phenomenon of bending and scattering when the wave deviates from the original straight line when encountering obstacles. Diffraction phenomenon in the insurance market can be manifested as the spread and diffusion of information in the market. Insurance companies transmit product information and selling points to consumers through different channels. In the process of continuous dissemination and diffusion in the market, such information may also be changed or misinterpreted under the influence of consumer feedback and word of mouth. Diffraction phenomenon makes the information and influence of insurance products expand and spread in the market in an unpredictable way, thus affecting the decision-making of consumers and the dynamics of the market.
In quantum physics, perturbations may significantly alter the frequency and amplitude of waves. The insurance market is also very sensitive to such sudden changes. Industry-wide responses to emerging risks, advances in product development, and shifts in consumer demands create a wave-like impact, leading to shifts and reaching a new equilibrium state in insurance offerings and market patterns. Traditional actuarial evaluation often lacks consideration for the wave characteristics of the insurance market. We need to adopt more flexible and elastic methods when evaluating risks. Quantum actuarial may be a new exploration direction.
On the other hand, within this undulating tide of the insurance market, each insured, as an actuarial particle, has different physical states and risk preferences, which means it has unique particle characteristics. Making a simple analogy, we regard the insured as an atom, the initial state of the insured as an atomic nucleus, and the insured's insurance needs as the electrons surrounding the atomic nucleus. When there is no energy absorption, the electrons will only be in the original energy level and will not transition. Like electronics, when the insured's risk preference or economic income is stable, there will be no new insurance needs injected into the system, that is, their insurance needs will not change and will not transition on different energy levels. On the contrary, after absorbing energy, electrons can also transition from one energy level to another. Similarly, when the risk preference or financial status of the insured changes over time, certain protection needs will be generated or released in the system, resulting in changes in the insurance needs of the insured.
There are many such cases in insurance practice. For example, let’s observe the change of the insurance needs of a young insured. It is not difficult to see that young people are usually in a low-risk state and may need less insurance protection. It can be analogous to how electrons move in the grounded state. However, with the increase of age and family responsibilities, the insurance demand of the insured will change accordingly. Just as the electron can jump to a higher energy level orbit, the insured may need more comprehensive insurance protection to meet the broader risk needs of individuals or families. These increased insurance demands can be seen as the transition of electrons from one energy level to a higher energy level. In addition, the insurance demand of the insured may also be affected by external factors. Just as the energy level transition of an electron will be affected by external energy, the insured's insurance demand will also change in the event of natural disasters or economic environment changes. This change can be likened to an electron that is excited to a new energy level under external stimulation.
Just as particles display quantifiable properties such as mass and charge, actuarial particles have specific attributes that shape their insurance requirements. They engage with different insurers, seeking the most suitable coverage, policy terms, and premium rates. The interaction between customers and insurers can be compared to the result of the collision and interaction of particles within the wave. This particle-like behavior can also be observed in claims settlements. When an insured event occurs, it becomes an individual transaction between the customer and the insurer, akin to a particle interacting with its environment. The insurer assesses the claim, evaluates the associated risks, and determines the settlement amount. Once settled, this transaction fades away, much like particles dispersing after interaction.
Acknowledging this wave-particle duality in the insurance industry can provide valuable insights for insurers and insured alike. For insurance companies, this dual perspective calls for a balance between macro-level market analysis and micro-level customer-centric approaches. While insurers grapple with the macroscopic market waves, they must effectively analyze and cater to the specific needs of individual customers, treating them as discrete particles. By using quantum actuary, insurers can discern market trends, identify patterns, and anticipate cyclical changes. Simultaneously, personalized risk assessment, tailored products, and efficient claims settlement processes address the discrete particle-like attributes of each individual customer’s benefits.
Unveiling the Uncertainty Principles of Insurance
One of the core aspects of insurance revolves around assessing and managing risks. Obviously, there is always uncertainty in insurance. The parallel between the Heisenberg Uncertainty Principle and the insurance market lies in the dynamic nature of both systems. Insurance is greatly influenced by economic factors such as interest rates, inflation rates, and employment levels. Additionally, changing regulations, legal developments, and consumer expectations further compound the uncertainty. Heisenberg Uncertainty Principle suggests that determining the exact set of risks associated with insurable events is remarkably difficult. These ever-evolving variables make it challenging for insurance companies to accurately predict market trends and evaluate pricing.
The Heisenberg Uncertainty Principle dictates that the more precisely we try to measure a particle's position, the less information we have about its momentum and vice versa.
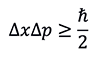
where ℏ is the reduced Planck constant, position (x) and its momentum (p) are called quantum pairs. When the position of a particle is measured, the observed photons will give the particle a momentum impact, which leads to great uncertainty in the momentum of the particle after measurement. In order to measure the position more accurately, a higher energy photon will be required, but it will give a greater impact to the measured particle, resulting in greater uncertainty of momentum.
So, are there similar quantum pairs in insurance? For example, loss ratios, which express the relationship between premiums earned and claims incurred, are the most crucial metrics for insurers. However, just as the uncertainty principle introduces limitations to precise measurements in quantum physics, insurers face statistical uncertainty in determining loss ratios. Insurers may base their projections on historical claims data, but unexpected catastrophic events, medical development, technological progress, and climate change can significantly disrupt the accuracy of such calculations. In quantum physics, momentum is the partial derivative of position with respect to time. Analogous to the insurance market, taking the incidence rate of COVID-19 as an example, the derivative of the incidence rate of COVID-19 is actually the transmission rate of COVID-19. Therefore, we can obtain the following inequality.

where qCOVID-2019 is the incidence rate of COVID-19, v is the transmission rate of COVID-19, c is the Planck constant for the COVID-19.
Through the above inequality, we can infer that the incidence rate of COVID-19 and its transmission rate could be a pair of quantum pairs. If we want to measure the incidence rate of COVID-19 more accurately, we need to more carefully detect whether COVID-19 exists in actuarial particles. Such observation behavior of large-area nucleic acid testing is likely to lead to the possibility of the wrong prediction of the spread rate of COVID-19 due to the gathering of testers, improper protective measures, lagging detection results and other reasons, so the measurement of the transmission rate of COVID-19 is more inaccurate. The Heisenberg Uncertainty Principle reminds actuaries that they need to handle and predict risks carefully to avoid over reliance on specific measurement results. Similarly, although we may try our best to collect a large amount of data and use complex statistical models when we prepare the incidence rate of life table or critical illness table, the measurement results are still uncertain due to the uncertainty principle. We need to be aware of this uncertainty and make reasonable adjustments and risk management when preparing the incidence table. Although we cannot completely eliminate uncertainty, we can manage and reduce the impact of uncertainty through reasonable data collection, model adjustment and scenario analysis. Acknowledging the Heisenberg Uncertainty Principle's influence in the insurance market will help insurance companies correctly understand the inherent uncertainty of insurance risk, so as to constantly adjust and optimize risk assessment and pricing methods with more robust and adaptable ways.
Conclusion
To explain how quantum physics could be used in insurance, we attributed several quantum characteristics to the insurance market to explore the correlation between them. The concepts of actuarial particle and Schrodinger's insured were introduced to better understand the unique features in quantum actuary, which have subverted the traditional insurance cognition. Understanding the wave particle duality in the insurance industry can enable insurance companies to achieve a balance between macro-level market analysis and micro-level customer-centric approaches. The Heisenberg uncertainty principle helps insurance companies correctly understand the inherent uncertainty of insurance risk. Actuaries should find a new method for risk assessment, choose a better quantum model to quantify the risk error, and find a way to coexist with such uncertainty. While reshaping the new pattern of insurance cognition, quantum actuary also guides the new exploration direction for risk assessment and product pricing. Quantum actuary could gain a competitive edge by enhancing risk assessment and predictive modeling capabilities. It could also have the potential for innovation and new product development. By embracing quantum actuary, insurers can stay ahead of the curve, delivering more accurate and tailored insurance products and services to their customers in a rapidly evolving risk landscape.
Statements of fact and opinions expressed herein are those of the individual authors and are not necessarily those of the Society of Actuaries, the newsletter editors, or the respective authors’ employers.
