Actuarial Teaching Conference: Using Keywords to Improve Learning and Instruction
By Russell Jay Hendel
Expanding Horizons, April 2023

This article presents a simple keyword technique facilitating the solution of verbal exam problems. Reading this article is sufficient to master the technique. With this mastery, a classroom instructor, a textbook writer or a resource for exam preparation will be able to add a few sentences in the material they produce to prevent some students who might otherwise fail to receive a grade of C or to raise a C student to a B student.
The literature on keywords is extensive. Even for teaching how to solve mathematical verbal problems in elementary school, there is controversy on whether keywords are good or bad, whether they help or hurt, and whether they should be used or not. Therefore, this article discusses both what one should do and what one shouldn’t do with keywords.
General Reading Theory—Importance and Strategies
Prior to discussing the keywords strategy, we will discuss its parent categories, verbal problems and reading.
The ability to solve verbal problems, whether mathematical or actuarial, is an important predictor of adult employment and wages. But solving verbal problems, even at the K–12 level, is challenging; it is challenging even to adolescents and adults.[1]
Consequently, modern pedagogy requires word-problem skills as an important component for the syllabi of K–12.[2] Certainly, this is true for the actuarial exams. But paradoxically, as of 2023, the SOA Exam syllabi, except for requiring students to recognize certain terms (keywords?) and apply certain concepts, do not explicitly mention verbal problems in either their learning objectives or their learning outcomes.[3] (There is no statement, for example, of the form “The candidate is able to apply principles for both computational and verbal problems.”)
Successful reading strategies do exist and do work. Two very successful strategies are (1) problem schema[4] and (2) textual organization structure.[5] Many instructors already use these techniques in their teaching.
Problem schema are popular with instructors, textbook writers and software designers who create practice software for actuarial exams. The term refers to providing students with a classification, or a scheme, of problem types (e.g., annuities can be level, arithmetic, geometric, or of mixed types). Textual organization structure alerts students to the general type of problem (e.g., comparison problems such as two annuities with equal present value, or sequence problems such as a reinvestment problem where the overall yield of a multistep process must be calculated).
Keywords
The keywords strategy simply refers to the instructor teaching, and/or the student being aware, that certain words in problems have specific meanings and translations into algebraic operations. Therefore, knowledge of keywords facilitates the student transforming the verbal problem into an algebraic problem, which is typically easier to solve.
Thus, keywords is a strategy that supplements other general strategies such as schema and textual organization structure. But if so, what is the controversy about using them?
Paradoxically the problem arises because many resources, instructors and students view the keyword-algebra correspondence as 1:1. Each keyword is supposed to refer uniquely to some algebraic operation. Such a viewpoint can actually be detrimental to problem-solving ability. Here are a few punchy, cute examples from K-12 literature. They were obtained merely by surfing the Net.
- Example 1: Does the keyword altogether refer to addition or multiplication? Consider: (1) Mary had 12 green apples and was given 7 more. How many does she have altogether? (2) John has 7 cartons of eggs, each of which has half a dozen eggs. How many does he have altogether?
- Example 2: Does the keyword phrase how many more refer to subtraction or division? Consider: (1) Sammy’s mother insists on him having 3 drinks of milk today. He has had one so far. How many more are needed? (2) One hundred students are going on a trip. Each bus has 40 seats. How many more buses are needed?
- Example 3: Does the keyword left refer to subtraction or addition? Consider: (1) Julie left $9 on the table. Her brother took $6 from the table. How much money was left on the table? (2) Julie left $9 on the table. Her brother left $6 on the table. How much money was left on the table?
We can now understand why one approach of the literature to these examples is that keywords should not be taught at all since they are harmful. Instead, students should be encouraged to develop critical reading and thinking skills and not rely on simplistic crutches that may only have value in a handful of problems.
Are General Thinking Skills an Alternative?
However, telling students to solve verbal problems by critically reading and thinking is not an adequate solution. Instruction, pedagogy and learning should follow good techniques of goal-setting.[6] Goal setting prefers subgoals that are simultaneously challenging, yet specific and unambiguous, with mastery achievable in a short time. Critical reading and thinking are general, not specific. They also are not masterable in a short time. In contrast, the keyword strategy is very specific; mastery of its use can be achieved relatively quickly.
Prior to reexamining keywords using the concept of goal setting, we observe that the two general reading strategies mentioned earlier—problem schema and textual organization structure—meet goal-setting criteria. For example, a student using problem schema is taught first to classify a problem as belonging to one of several key areas and subareas and then to apply the techniques of those subject areas to solve the problem. This is specific, unambiguous, challenging, and masterable in a short time.
Keywords with Multiple Meanings
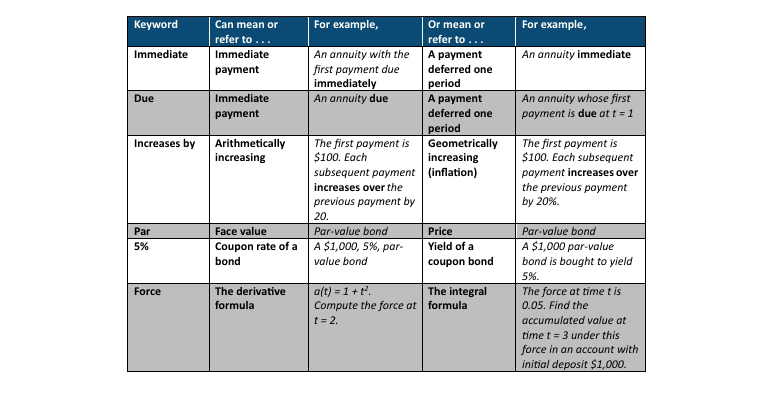
The approach suggested by this article to redeem the keyword strategy, making it useful and successful, is to teach that keywords may have multiple algebraic meanings. The student’s task when seeing a keyword is to recall its multiple meanings and decide which one is appropriate for the given problem. To illustrate this technique, Table 1 presents several keywords with multiple meanings from the Society of Actuaries (SOA) Financial Mathematics Exam (Exam FM) syllabus.[7] It is assumed that the reader is familiar with them.
Table 1
Keywords in the SOA FM Syllabus That Have Multiple Meanings
Furthermore, it is not sufficient with the keyword strategy to simply give students a list of words and their multiple meanings. Students must be taught how to tell which meaning is operative.
The following illustrative contrasts, none of which explicitly exist in any current textbook, should be part of the instruction, textbook narratives, and problem-software guidance accompanying the presentation of keywords.
- Example 1—Increase by: Increasing by a percent indicates geometric growth (inflation), whereas increasing by an amount indicates arithmetic growth. Additionally, students should, in this connection, be taught the reason for using basis points (to indicate arithmetic growth).
- Example 2—Force: There are two formulae associated with force. If you know the accumulation function but don’t know the force, you use the derivative formula (δ = dA/dt); if you are given the force but don’t know the form of the accumulation function, you use the integral formula (A(t) = eꭍδ ds).
- Example 3—Coupon vs. interest rate: a percentage that is used adjectivally for a bond (i.e., preceding the word bond) refers to the coupon rate, not the interest rate (yield).
Keywords, which as indicated above are not meant to be one-step processes that require substitution of a formal algebraic symbol for an English word, are analogous to the street corners encountered during a drive in a car: Although driving a car is straightforward along each block, at corners, one must stop, think, look around and evaluate: Should one go straight or turn? Should one wait till the traffic signal allows one to proceed? Keywords are analogous to such corners in a drive. They require that the candidate stop, think, look around and evaluate.
Furthermore, the keyword strategy is superior to general critical thinking because it meets the goal-setting criteria of specificity and achievable timely by providing the candidate with several very specific, reasonable alternatives and guidelines for what to do.
At this point we can repeat the goal of this article: Reading this article is sufficient to master the keyword technique. With this mastery a classroom instructor, a textbook writer or a resource for exam preparation will be able to add a few sentences in the material they produce to prevent some students who might otherwise fail to receive a grade of C or to raise a C student to a B student.
We also emphasize that this compilation and presentation of keywords, along with the guidelines for distinguishing multiple possible referents of a keyword, are the responsibility of the instructor—not the student.
Advanced Use of Keywords
The literature, even that for K–12, is quick to point out that not all problems have keywords. A simple K–12 verbal problem without keywords is “How many legs do 6 elephants have?” Despite the lack of universality of keywords, they still can be useful even for problems without them. This section provides an illustrative example using Bayes theorem, a topic covered in the SOA Probability Exam (Exam P) syllabus.[8]
Table 2 presents three versions of the same problem.[9] Notice, that version 1 can be translated almost verbatim from English to algebra, as shown in the second row. For example, the English sentence “The probability that it is cloudy in the morning given that it rains that day is 75%” can be reformulated algebraically by translating the keyword given as a vertical bar (|) and the keyword is as an equal sign (=); these substitutions directly and immediately yield, Pr(Cloudy|Rain) = 75%. In contrast, versions 2 and 3 do not allow an immediate and direct translation using keywords. In other words, the keyword technique only works nicely for version 1.
Table 2
Three Versions of the Same Problem (Only version 1 is amenable to keywords.)
Table 2 suggests the strategy that the author in fact uses when teaching verbal problems:
- I first survey as many books on a given topic as possible to gather all verbal problem types associated with it.
- I select the verbal problem type that can be solved with keywords. If none exists, I create one.
- My teaching strategy is to initially present this special problem that can be solved by simple keyword translation.
- I then present, as time permits, the other versions of the verbal problems. I show how the other versions can be translated into the initial keyword-solvable form and discuss how to identify each version type.
I have found this method successful. Typically, weaker students benefit from comparing and contrasting problem types. Stronger students, while not needing the crutch of keywords, benefit from seeing a wide variety of problem types.
Conclusion
In the teaching of verbal problems for actuarial exams, this article has presented the keyword technique as a supplemental strategy to the main verbal problem techniques, such as problem schema and textual structural organization. The keyword strategy presented here improves on the literature version of keyword strategy simply by allowing each keyword to represent multiple possible algebraic translations. The article also advocates identifying guidance rules for selecting particular algebraic translations of keywords. The keyword strategy is even useful for introducing verbal problems that cannot be solved by keywords. Specific preparations and class instruction should be used with the keyword strategy. I believe the methods of this paper will benefit instructors.
Statements of fact and opinions expressed herein are those of the individual authors and are not necessarily those of the Society of Actuaries, the editors, or the respective authors’ employers.
Russell Jay Hendel, Ph.D., ASA, is the chair of the Education and Research Section council. He is adjunct faculty III at Towson University, where he assists with the Actuarial Science and Research Methods program. Russell can be reached at RHendel@Towson.edu.