Real Options in Radical Uncertainty: Part 2—The Limits of Financial Option Theory
By Bryon Robidoux
Risks & Rewards, September 2023

This article will focus on when to use financial option theory versus real options under radical uncertainty. This article was inspired by the book Real Option Analysis and Climate Change: A New Framework for Environmental Policy Analysis. Understanding how to make decisions related to climate change is a crucial problem. But taking a step back and thinking about decision-making policies for climate change, they have similarities to insurance problems with market guarantees. They are both radically uncertain and can be very long-dated. They are also dependent topics because if climate change is terrible enough, ecosystems die, taking some of humanity with them, the markets tank, and guarantees explode!
Part 1 Recap
Part 1 of this article deeply explored the origins of risk and uncertainty, which are vastly different. They have very distinct characteristics.
The properties of risk are:
- Applicable to casino managers, not actuaries.
- Relevant only to games of chance like Yahtzee, Poker, and Blackjack.
- Everything about the event space is known with certainty because casino managers created it for a fictitious world.
- All participants understand the rules before any experiment begins, and the rules never change. They also know precisely what the outcomes are and can calculate with certainty the probability of each outcome.
- The energy requirement for the outcomes is immaterial.
- Correlation is the measure of dependence.
The properties of uncertainty are:
- It is the actuary's lifeblood.
- It is applicable to the real world, which includes everything outside of man-made constructed games of chance.
- The event space is infinite, instantaneously changing through universal innovation, only constrained by the laws of physics, and cannot be known with certainty.
- Humans have minimal control over the event space and such control is due to laws and regulations, which only apply at the ease of enforceability.
- Determining an event's likelihood requires knowing the relative energy necessary to produce it.
- The less energy required to produce an event, the more likely it is to happen.
- Dependence describes the degree of connectedness between events; the more substantial the connection, the easier it is to transfer energy.
- Practitioners create and model arbitrary event spaces to make problems tractable based on the problem's context.
- The practitioner may never know the reason for an outcome.
To Be Gaussian or Non-Gaussian, That is the Question
Three families of distributions describe a vast majority of the observed phenomena:
- The Gaussian or normal distribution,
- family of exponential distributions (these will not be covered in this article for brevity), and
- power law/heavy-tailed distributions.[2]
Gaussian
The Gaussian distribution is most famously associated with the central limit theorem. The central limit theorem should be renamed the center limit theorem because it deals with the center of the distribution.[3] The central limit theorem states that for independent and identically distributed samples, the sample mean merges with the normal or Gaussian distribution even if the original samples are not normally distributed.
The Gaussian distribution also has some very convenient properties:
- It can be completely described with only two values: The mean and standard deviation.[4]
- Any linear combination of Gaussian random variables results in a Gaussian random variable.
- There is an analytical closed-form solution to estimate unknown linear Gaussian parameters.
- The estimation of unknown parameters is a linear function of the measurements.[2]
- The likelihood of deviation from the average or center of the distribution exponentially decreases with the amount of deviation.[4]
These convenient properties encourage modelers to flock to the Gaussian distribution even when it is not appropriate.[4] Examples of its extensive usage can be found in the statistical modeling of Brownian motion, census data, and student grades.[2]
Power Laws/Heavy-Tailed Distributions (HTD)
HTDs are designed to model complex systems where the system elements are highly connected. This ability makes them more suitable in modeling extreme events. The likelihood of significant events is much greater in heavy-tailed distributions than in a Gaussian distribution. Power laws apply to many observable phenomena including personal wealth, corporate profitability, price variations, train derailments, forest fires, wars, and other conflicts, to name just a few.[2].
A power law distribution is one in which the likelihood p(x) of a particular size of the event (x)
is proportional to that size raised to the negative of some power y
: That is, p(x) ∝ x-y
. As x -> 0, the frequency of events increases. In practice, to make the function a little better behaved, the domain of x is restricted to
(1,∞), and this is called the truncated power law. Nearly all power laws use an exponent range of
1≤y≤3.[2]
Economic practitioners hesitate to use HTDs because it is difficult to apply them based on historical outcomes. There is always another extreme event on the horizon that skews the previous results.
- The good news is that the median and exponent of a power law are estimable from the data, but
- The bad news is that the maximum and mean are not reliably estimable.
For example, imagine calculating the average compensation of all Amazon warehouse workers. Now suppose Jeff Bezos was added to the calculation!
The mean and variance also present another potential problem, as illustrated in Table 1.
Table 1
Mean and Variance Potential Problem
With infinite variance, the modeler may never have enough data points to calculate the sample mean.[2] This problem is exacerbated by the Weitzman effect, which is the observation that if the power law exponent is not known with certainty or results in a fat-tailed distribution, the speed at which the probability of extreme events tapers off decreases. However rare, the events in the tail may become more frequent than a superficial reading of the parameters defining the tail may suggest. The deeper one goes into the tail, the more pronounced the effect.[1]
Real Options Analysis
The mathematical background information discussed above facilitates the application of real options analysis. Real options help practitioners know when to expand, wait, defer, or abandon a project. It is commonly taught that financial options give the buyer of an option a right, without obligation, to do something. For financial options, this right could be to buy or sell a good at a specific price sometime in the future. For options not traded in the market and made under uncertainty, this definition of an option can be generalized as measuring the expected benefit the purchaser can receive by owning it. As applied to investing under uncertainty, it is the potential benefit of making a particular investment.[1]
In 1973, Myron Scholes, Robert Merton, and Fischer Black created the Black-Scholes formula. In 1977, Stewart Myers realized that options can be used to value corporate investment within a firm. He coined this application “Real Options Analysis.” While Myers thought that it was magnificent to use the Black-Scholes formula for this use, practitioners found it to be largely impractical when applied. There are three requirements for the Black-Scholes formula to be applicable for use:
- First-degree homogeneity,
- uncertainty must derive from Brownian motion, and
- risk neutrality.[1]
First-Degree Homogeneity
First-degree homogeneity requires that the value of an option for k shares is k times the value for one share, ceteris paribus. Mathematically it implies that H(λX,λY,T)=λH(X,Y,T), where:
λ is a scalar.
X is the underlying asset.
Y is the exercise price.
T is the exercise time.
H(X,Y,T) is the option value.
First-degree homogeneity is not a universal property for options in uncertainty, such as mitigating greenhouse gases. Doubling the cost of a policy will not reduce emissions by a factor of two or divide the environmental damage in half.[1]
Uncertainty Derived From Brownian Motion
According to John C. Hull in Options, Futures, and Other Derivatives:
"Brownian motion is a Markov stochastic process with a mean change of zero and a variance rate of 1 per year. A Markov process is a particular type of stochastic process where only the present value of a variable is relevant for predicting the future. The history of the variable and the way that the present has emerged from the past is irrelevant.
“Predictions of the future are uncertain and must represent a probability distribution [which is assumed to be Gaussian]. The Markov property implies that the probability distribution of the price at any particular future time is not dependent on the specific path in the past. This property is consistent with the weak form of market efficiency. If the weak form of market efficiency were not true, technical analysts could make above-average returns by interpreting charts and the history of stock prices. There is very little evidence that they can do this.”[5]
Financial market theory assumes that investors live in a risky world where they know everything about the event space and its probability distribution. But there is a vast difference between risk and uncertainty, which makes Hull’s comments above only valid inside the walls of the casino. They no longer hold when stepping outside of the casino and into the real world.
Uncertainty Derived from Universal Innovation
With universal innovation, the path taken in the past is entirely relevant, consistent with Mandelbrot's research findings that markets have memory ranging from weak to strong.[10] The infinitely recursive process of combining past information into novel solutions through computation produces the current state. The memory of universal innovation is the change in energy required for novel combinations and their dependencies on past states. As innovation occurs, the same outcome requires less energy because the information solidifies previous computations' results. For example, building a Tesla Roadster in 1953 would take way more energy and resources than in 2023.
Since universal innovation derives from a minimum criteria novel search (MCNS) within an infinite event space that instantaneously changes, it ultimately thwarts the ability to analyze past information to predict the future. Therefore, the weak form of market efficiency is not true because of the lack of stationary and independent time increments.
Furthermore, technical analysis does not provide any insight into the MCSN algorithm. The word “novel” is included in the title of the algorithm, which implies that events will not develop in the future like they did in the past. Hence, there is no evidence (that was not tortured[8]) that technical analysis can successfully predict the future! Technical analysis is the idea that one can count cards in the real world outside of the casino. Therefore, market efficiency is false and technical analysis serves no purpose.
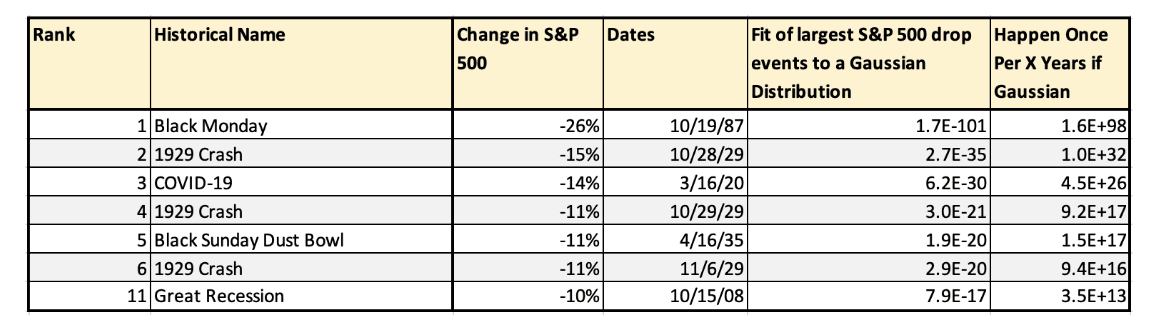
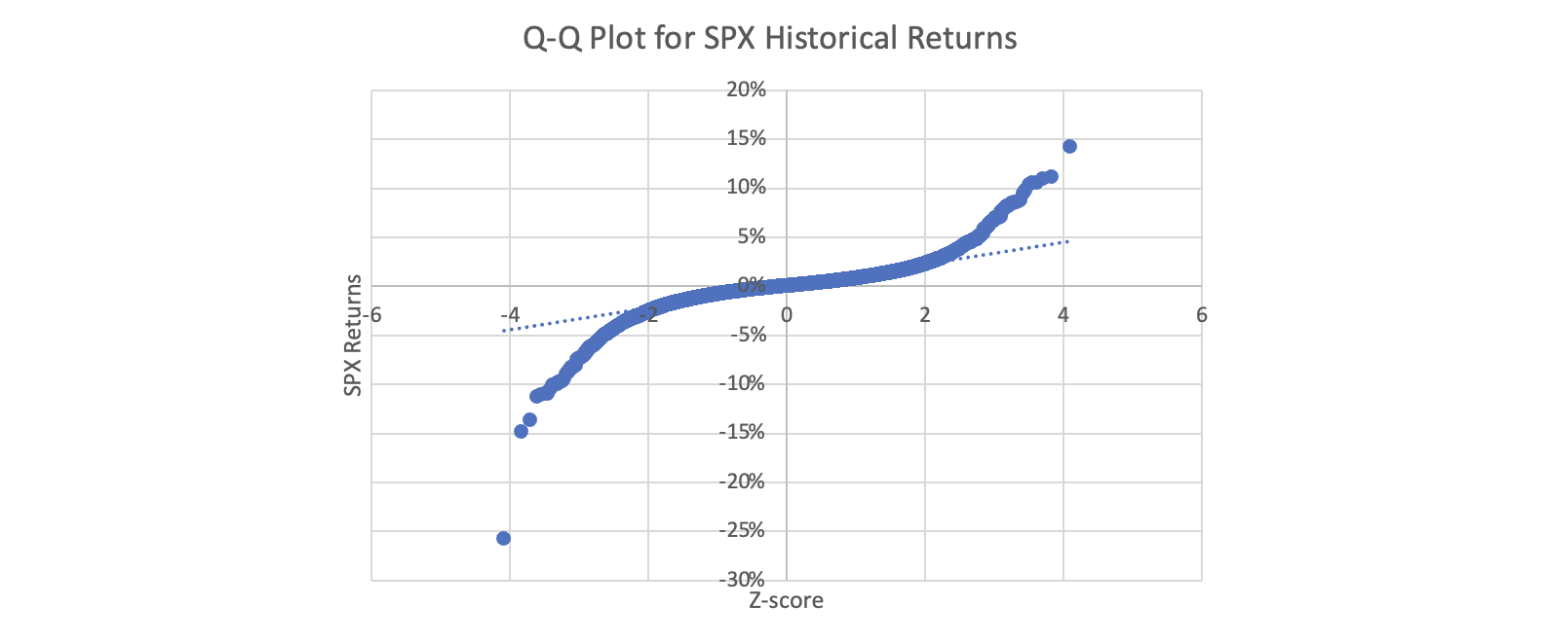
These facts flip the result of event evolution from being independent to highly dependent on the past and its path. This flip demonstrates how physics can be used to show why the probability distribution of market prices much better fits a power law[2,3,4] than a Gaussian distribution. It is the nature of uncertainty and the path-dependent MCSN algorithm. Nicholas Nassim Taleb’s observations in this regard are particularly salient; one might not be able to prove a distribution uses a power law due to the lack of historical data. However, one only needs a point or two to verify the distribution is not Gaussian.[4] (See Table 2 and Figure 1)
Table 2
Non-Gaussian Distribution
Figure 1
Fit of SPX History for the Gaussian Distribution
Risk Neutrality from a Risk Perspective
A risk-neutral investor is an agent indifferent between a guaranteed payoff and a risky bet with an expected payoff equal to the guaranteed payoff. The concept of risk-neutral is undefined in an uncertain real world. Prospect theory provides empirical evidence for this assertion.
From Investopedia, "Prospect theory assumes that losses and gains are valued differently, and thus individuals make decisions based on perceived gains instead of perceived losses." The classic example demonstrating this is taken from the book Behavioral Finance:
"Scenario A is in addition to what one already owns, one receives $1000 for sure and either:
- Receives another $500 with certainty, or
- has a 50% chance of receiving nothing and a 50% chance of receiving $1000.
Scenario B is in addition to what one already owns, one receives $2000 for sure and either:
- Loses $500 with certainty, or
- has a 50% chance of losing nothing and a 50% chance of losing $1000.[9]"
In the lab, most people pick the first option in scenario A and the second option in scenario B. Still, all scenarios and all possibilities lead to the same expected value of outcomes of $1500, so the participants should be indifferent and have an even blend of options one and two. Prospect theory says that they appear to be risk-averse in scenario A but risk-seeking in scenario B, which oddly has them changing their behavior based on the framing of the question.
However, prospect theory arrives at this conclusion only because it assumes that people live in a risky world based on Gaussian distributions. The only way the participants can reliably calculate the expected value is if the participant knows the probability distribution with certainty. The assumption is Gaussian because the expected value is always defined. Prospect theory is casino logic. Actuaries know that assumptions are everything! Everything!
Risk Neutrality from a Radically Uncertain Perspective
But in an uncertain world, the event space is not fully defined and continuously changes. Furthermore, people may not be able to calculate the expected value because:
- Uncertainty is subject to power laws,
- the expected value can be ±∞
, and
- history is not a reliable indicator of expected value.
Therefore,
- In scenario A, what should one do if one is given a certain outcome of $500 or an expected value of $500—which cannot be reliably calculated?
- One should take Steve Miller's advice and "take the money and run."
- In scenario B, what should one do if one has an inevitable loss of $500 or an expected loss of $500—which cannot be reliably calculated?
- One should bet the farm and hope a very unlikely but huge tail payoff will make the expected loss a gain.
What is the fundamental flaw with prospect theory and risk preferences? It assumes that one knows the underlying probability space with certainty, which means that certainty and the expected value contain the same amount of information, which leads to indifference between them when the expected value equals the certain value. In an uncertain world, certainty holds complete information; there is less information in the expected value because people cannot reliably calculate it.
People are not changing choices due to some fictitious concept of risk preference but rather due to their information preference. People are always attracted to gains and always repel losses. It is certainty versus uncertainty they are reacting to in both cases. Certainty holds more information, and therefore more value when making decisions.
Claude Shannon beautifully described information as a physical concept in the 1940s. Going deeper, Maxwell's demon relates information to energy, and energy is everything in an uncertain world! The real world works as it should because people behave according to their respective physical realities and not within economically contrived situations.
What are the true lessons of prospect theory?
- People evolved to live in an uncertain real world governed by power laws, not a risky fictitious one ruled by the Gaussian distribution.
- Applying behavior derived from risky situations and using them in uncertain conditions is entirely erroneous because they produce different answers regarding the correct decision.
- It is dangerous to assume one knows things that cannot possibly be known, such as the likelihood of outcomes under radical uncertainty, because this will cause the practitioner to veto his gut reaction, which has evolved over millions of years.[7]
- There is no concept of risk-averse, -neutral, or -seeking outside of a casino because the ideas require a world containing a known probability distribution and estimable expected value.
- People make decisions based on their information preferences and not risk preferences.
What Does This All Mean?
The purpose of this journey was to find the boundary point of when Black-Scholes and financial options theory are no longer relevant because this understanding provides the insight needed to deal with decisions around climate change and other radical uncertain events. The relegation of financial option theory to being inside the walls of a casino was not anticipated. But with a combination of elementary physics, information theory, complexity theory, and data science, relegation is the result because they help describe the true difference between risk and uncertainty. If an economist and physicist are in a death match together, the smart money will be on the physicist! An economist usually says how something should work, while a physicist normally will say how something does work.
There is hope. All the path requires is to go from team Black-Scholes and Friedman[7] to team Mandelbrot and Keynes.[4] Mandelbrot has spent many years developing fractal finance, which replaces the risk-based Gaussian conclusions and translates them to uncertainty and power laws.[3,4]
Mandelbrot has saved actuaries from needing to start from scratch. But moving forward, actuaries will best serve their clients, employers, and profession in fulfilling their duties by ending the development of byzantine regulation on top of theories derived from unapplicable artificial worlds founded on assumptions of things that humans cannot possibly know. Actuaries should step out of the casino and into the light by creating more straightforward regulations grounded in option analysis under radical uncertainty, fractal finance, and complexity theory. These subjects account for real world realities to manage the unknown and unknowable uncertainties in insurance and climate change.
Statements of fact and opinions expressed herein are those of the individual authors and are not necessarily those of the Society of Actuaries, the newsletter editors, or the respective authors’ employers.
Bryon Robidoux, FSA, CERA is assistant vice president of Product Development at Constellation Insurance. He can be reached at bryon_robidoux@ConstellationInsurance.com.