Managing Investment Risks in Contractual Designs
By Runhuan Feng and Longhao Jin
Risk Management, September 2021

Life and annuity markets around the world have seen increasingly complex investment-combined products, including universal life, fixed indexed annuities, variable annuities with a wide variety of guaranteed benefits and indexed variable annuities. Insurance companies are facing unprecedented exposure to financial risks in addition to traditional mortality and longevity risks. The risk assessment and modeling for such complex designs by conventional methods often focus heavily on their market competitiveness and profitability. However, there seems to be a lack of quantifiable and systematic approaches to assess investment risks associated with investment combined products. The objective of the proposed work is to develop a framework for quantifying and analyzing various forms of contractual designs and showcase different techniques to assess the trade-off between competitive contractual designs and their practical implications regarding the difficulty of risk management.
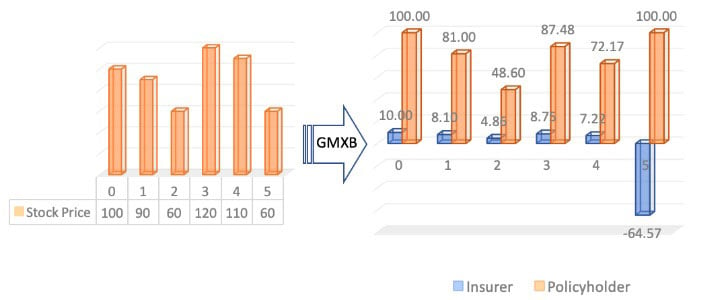
As a general principle, we think of a contractual design as a mapping from the dynamics of the underlying risk(s) to an insurer's financial obligations. Suppose an investor has $100 to invest either directly in a stock or in a variable annuity contract linked to the same stock.
The left panel of Figure 1 shows the evolution of stock prices over a period of five years. If left unprotected, the investor is fully exposed to equity risk and her investment varies exactly by the same amount as stock price. The VA contract offers a guaranteed minimum maturity benefit, which guarantees a minimum balance of $100 after five years. The cash flow is now split between the policyholder and the insurer who underwrites the variable annuity contract. The right panel of Figure 1 shows the new set of cash flows between the policyholder and the insurer. In compensation for the guaranteed benefit, the policyholder pays 10 percent of her account values on an annual basis to the insurer. From the figures, we know that even though the investor’s investment still varies in proportion to the stock price, she receives a boost to her investment due to a benefit payment from the GMMB at maturity. Therefore, the equity risk is partially transferred from the policyholder to the insurer, who receives annual fee incomes and carries the financial obligation to absorb some of the policyholder’s loss.
Figure 1
A Mapping From the Dynamics of Equity Risk to an Investment Guarantee
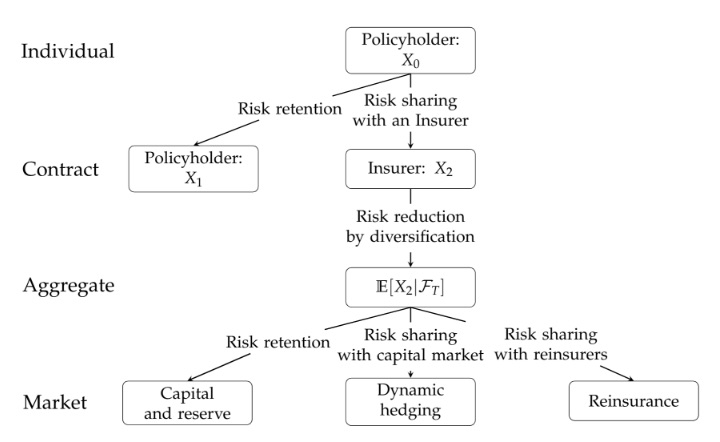
In general, there are four well-known risk management techniques: risk avoidance, risk reduction, risk sharing, and risk retention. The last three are often combined in various ways in contractual designs. Adding to the complexity is the interplay of various types of risks such as equity risk, inflation risk, and mortality risk. Figure 2 shows how risks are transferred among various stakeholders including policyholders, insurers, re-insurer, and capital market. This quantitative framework was developed in Feng (2018). Policyholders are more concerned about the risk transfer from policyholder to an insurer in the first step since it quantifies how much risk is reduced when they purchase a product. While the insurers pay more attention to the second and third steps, as they show the insurer’s capacity of coping with risks ceded by the policyholder. In the figure, X0 and X1 represents the policyholder’s financial position by purchasing the product without and with the guarantee respectively and X2 represents the insurer’s financial position by selling the product with the guarantee. The conditional expectation E[X2│FT ] gives the insurer’s financial position when the mortality risk is absorbed, where {Ft:0≤t≤T} represents the filtration with which a stochastic process {St:0≤t≤T} is defined and St is the market value of the underlying equity index or fund at time t. The filtration represents the accumulation of market information over time.
Figure 2
Effect of Risk Transfer at the Contract Level
There are three common types of guarantees in the market, which are guaranteed minimum maturity benefit (GMMB), guaranteed minimum death benefit (GMDB), and guaranteed minimum withdraw benefit (GMWB). We show the risk transfer at contract level as well as risk reduction at aggregate level by numerical illustrations. And we consider two different types of risks, namely equity risk and mortality risk.
The Effect of Risk Transfer at the Contract Level
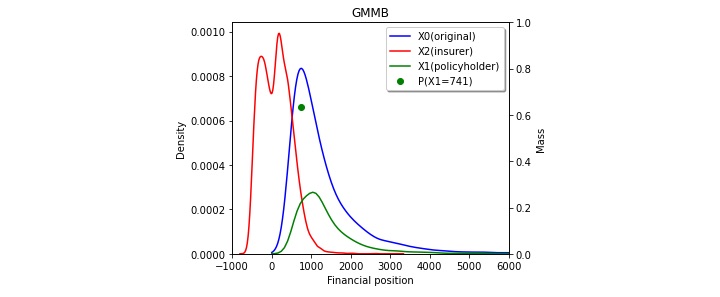
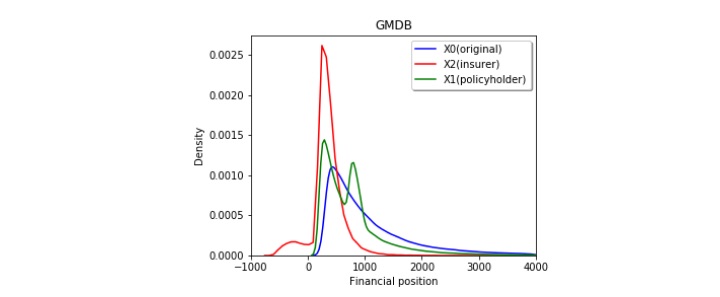
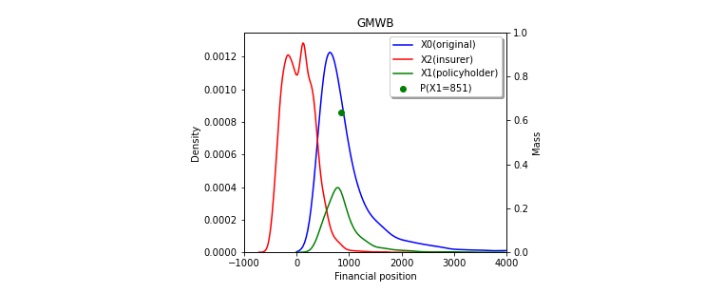
Figures 3a, 3b, and 3c show the risk-sharing effect of the GMMB, GMDM, and GMWB products. The red line shows the probability density function of the insurer’s financial position, and it can be shown in three figures that there are two peaks. In Figures 3a and 3b, the peak on the right shows the most likely range of fee incomes contributed by policyholders who survive to maturity. In Figure 3c, the peak on the right represents the case when there is a balance in the policyholder's account at maturity. The peak on the left indicates the most likely range of insurer’s net loss due to benefit payments. It is clear from the figures that the insurer carries most of the downside risk as its probability density function centers around near zero levels. The blue line and green line represent the investor's risk profile before and after purchasing the product. The probability mass of the green line shows the guaranteed amount of benefit paid to the policyholder. (Refer to the right side of Figures 3a and 3c for the scale for probability mass.) In GMMB and GMDB products, it is the guaranteed benefit payment if the policyholder survives to maturity and the investment account underperforms. Similarly, it is the guaranteed amount of full withdrawals by the policyholder in GMWB product. Besides, we know from all three figures that from the policyholder's perspective, she gives up some portion of upside gain in exchange for protection from the insurer for the downside loss. As expected, the account values for the policyholder with the guarantees turn out to be more concentrated (thinner left- and right-tails) than those without.
Figure 3
Effect of Risk Transfer at the Contract Level
Risk Reduction at Aggregate Level
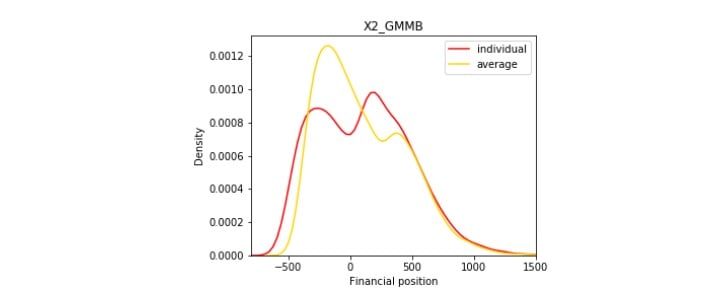
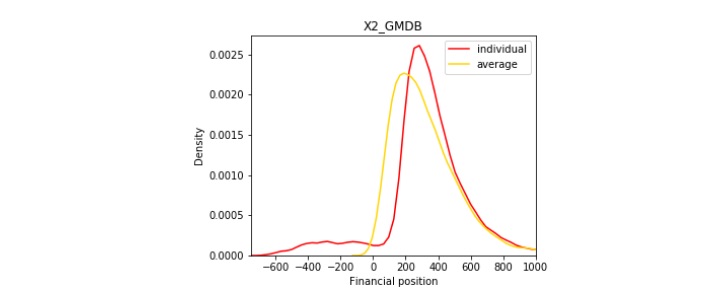
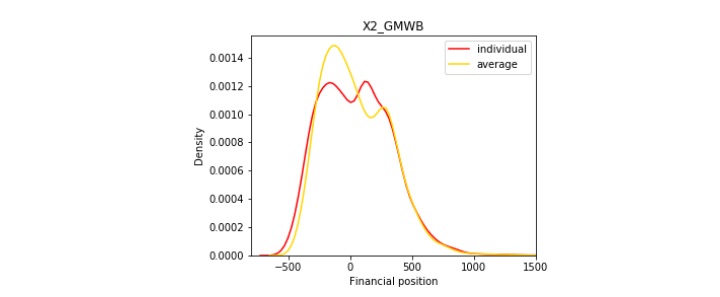
Figures 4a, 4b, and 4c show the risk reduction effect at aggregate level, where we assume there is a sufficiently large number of policyholders so that the law of large numbers applies and the mortality risk is completely diversified. In contrast to the yellow line, which is the individual liability at the contract level with undiversified mortality risk and equity risk, the red line represents the insurer's average liability at aggregate level with diversified mortality risk and undiversified equity risk. Due to the reason that extreme scenarios are more likely to happen with the interaction of mortality and equity risk, the yellow line is more concentrated than the red line.
Figure 4
Risk Reduction at Aggregate Level
c. GMWB
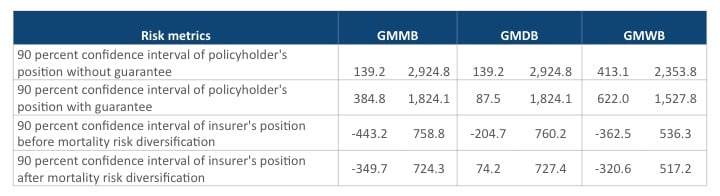
In summary, all three different guarantees offer the protection on the downside loss, but the policyholder gives up some portion of the upside gains. Moreover, after the diversification effect on the mortality risk, the risk has been reduced in the guaranteed annuities. To have a broader view of the contractual design, we compare three guaranteed annuities in Table 1.
From Table 1, we have the following observations. Firstly, we know from the first row that the GMWB has a narrower interval among the three, which means it provides a safer financial position to the policyholder without any guarantees. It is consistent with the product feature that the policyholder withdraws a certain amount of money from the account so that the policyholder's asset is less exposed to equity risk. Secondly, it can be found that the policyholder's financial positions without guarantee are identical for GMMB and GMDB. However, when we consider the case where the policyholder purchases the guaranteed annuity product, the situation is different. The lower bound of the confidence interval for the policyholder’s position with the GMMB is higher than that with the GMDB. This is because the policyholder is likely to survive the contract period and is hence exposed to the equity risk after the GMDB expires, whereas the policyholder’s account is floored by the GMMB after the period. Since the chance the policyholder dies within the contract period is rather low, hence the policyholder is most likely to end up with account value without any guaranteed payment when the GMDB expires. The right tail captures favorable scenarios in which the account values outperform the guaranteed base under the GMMB. Hence the GMMB and the GMDB have the same right tail. The GMDB rider leads to narrowest confidence interval of the insurer’s profit. If confidence intervals before and after risk pooling are compared, we observe that the improvement is the smallest with the GMWB. It has to do with the fact that most individuals survive before the rider expires and the impact of mortality risk is rather small. The fact that the GMDB rider appears to be more profitable than the other two is because the policyholder has a relatively high probability of survival to maturity, 0.82, and hence the GMDB payments are not always needed.
Table 1
Risk Reduction at Aggregate Level
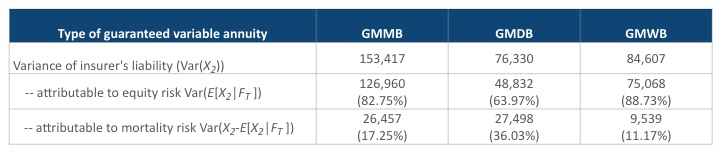
Table 2 offers a breakdown of the variance of the insurer's liability for each product type. As we have explained earlier, the insurer's liability after the pooling of mortality risk, E[X2│FT], is less than or equal to that prior to the pooling, X2, and hence the variance of the former is clearly smaller than the variance of the latter. It is also well known that E[X2│FT ] is uncorrelated with X2-E[X2│FT ]. The mortality risk is completely diversified in E[X2│FT ]. Therefore, it is natural to separate the variances, which are attributable to different sources. It is clear from Table 2 that mortality risk contributes the most to the variability of the GMDB liability and the least to that of the GMWB liability.
Table 2
Risk Analysis for Different Guaranteed Benefit
While the discussion above concentrates on the interplay between mortality risk and equity risk, we now consider another type of risk—inflation risk. Many insurance products offer inflation protection features, under which benefit payoffs increase periodically to keep up with inflation. Inflation protection features are common for products that offer benefits in the form of annuities, such as a cost-of-living adjustment on life annuity and disability insurance. Because these products are typically bought many years before the first annuity payment is drawn, the cost of living or care may have far exceeded its original estimate. Therefore, inflation protection is critical for policyholders to retain the real value of its insurance protection. While these features are considered desirable for policyholders, they can be difficult to manage for insurers. Detailed discussion can be found in Feng and Jin (2021), Feng and Yi (2019), Feng (2014).
The purpose of this work is to develop a quantitative framework in which we can quantify and assess the connection between various contractual designs and associated risks. We analyzed the interplay between the mortality risk and the equity risk in the common guaranteed annuity products and displayed the comparisons among them. In addition, we also provided a way of managing inflation risk for the insurers in the annuity market.
Statements of fact and opinions expressed herein are those of the individual authors and are not necessarily those of the Society of Actuaries, the newsletter editors, or the respective authors’ employers.
Runhuan Feng, FSA, CERA, Ph.D., is a Professor of Mathematics, Statistics, Industrial Systems and Enterprise Engineering, director of Actuarial Science, director of Predictive Analytics and Risk Management, the State Farm Companies Foundation Professorial Scholar at the University of Illinois at Urbana-Champaign. He can be reached at rfeng@illinois.edu. LinkedIn: https://www.linkedin.com/in/runhuan-feng-phd-fsa-cera-93589085/
Longhao Jin, Ph.D., is a candidate for University of Illinois at Urbana-Champaign. He can be reached at longhao2@illinois.edu. LinkedIn: https://www.linkedin.com/in/longhao-jin-316147a0/
References
Feng, R. (2014). A comparative study of risk measures for guaranteed minimum maturity benefits by a PDE method. North American Actuarial Journal 18(4): 445–61. doi: 10.1080/10920277.2014.922031.
Feng, R. (2018). An introduction to computational risk management of equity-linked insurance. Chapman & Hall/CRC Financial Mathematics Series. CRC Press, Boca Raton, FL.
Feng, R., and L. Jin. (2021). Managing investment risks of insurance contractual designs. Technical report, Society of Actuaries. https://www.soa.org/resources/research-reports/2021/contracutal-designs/
Feng, R., and B. Yi. (2019). Quantitative modeling of risk management strategies: stochastic reserving and hedging of variable annuity guaranteed benefits. Insurance: Mathematics and Economics 85: 60–73. doi: 10.1016/j.insmatheco.2018.12.003.