Stratégie de gestion du risque d’entreprise faisant intervenir la notion d’adaptateur
par M. Bruce Beck, D. Ingram et M. Thompson
Gestion du risque, avril 2022

Partie I
Les rouages du contrôle automatique par rétroaction en cascade
Étudier des données sur les risques de marché, sur le comportement des actifs financiers, sur les profits et pertes; formuler des recommandations; anticiper l’obtention de nouvelles données afin d’améliorer ou de mettre au point les recommandations pour la prochaine période de décision : voilà en quoi consiste la journée type de l’actuaire. L’ingénieur automaticien (ndlt : qui travaille au niveau de l’ingénierie des contrôles automatiques), quant à lui, passe le plus clair de son temps à étudier des boucles de rétroaction dans des « schémas fonctionnels », en fait, comme celui de la figure 1.
Aux commandes
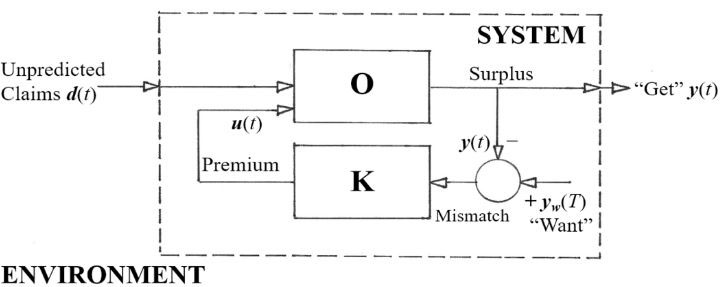
Les sinistres entrent par la gauche dans le cadre en tirets du « système » (l’assureur) de la figure 1, passant ainsi du domaine des risques possibles à l’environnement de risque de l’entreprise. L’actuaire recueille de l’information à propos de l’incidence de ces sinistres sur l’évolution de l’« excédent » de l’assureur, en se dirigeant vers la droite, puis détecte l’existence de « décalage » entre les objectifs de l’entreprise (flèche « Want ») et les résultats réels (flèche « Get »). En cas de décalage, la magie de l’actuaire s’opère à l’intérieur de la boîte « K ». Celui-ci recommande alors de modifier la prime demandée et transmet cette information vers la gauche et au niveau de la boucle; cette information devient alors un intrant des activités de la société d’assurances (la boîte « O »).
Figure 1
Boucle de contrôle automatique par rétroaction dans un schéma fonctionnel d’ingénierie du contrôle automatique. Le système illustré représente le processus décisionnel de fixation des primes d’un régime d’assurance rentable.
La première rencontre de l’actuariat et de l’ingénierie du contrôle automatique a eu lieu il y a longtemps, vers la fin de 1970 et le début de 1971, lorsque Bernard Benjamin, professionnel de l’actuariat, a rencontré par hasard l’ingénieur automaticien Les Balzer au laboratoire de contrôle automatique informatique de l’Université de Cambridge. Leur objectif était de stabiliser la performance financière du mécanisme de participation aux bénéfices d’un assureur face aux demandes imprévues d’indemnisation [1]. Ils y sont parvenus par simple manipulation graphique d’un schéma fonctionnel comme celui de la figure 1. Comme les temps ont changé!
Bien que la figure 1 ne dise pas grand-chose à la plupart des actuaires, les concepts qu’elle véhicule constituent le cœur de leur travail. Le problème est de savoir qui exactement est aux commandes du contrôleur représenté par la boîte K.
Mais avant tout : ne négligeons pas un principe fondamental de la théorie des systèmes sans rien dire
Notre monde s’est disloqué dans la figure 1 (cela se produira à nouveau plus loin dans la figure 3), du fait que l’on a extrait le « système » de tout le reste, c’est-à-dire de l’« environnement » dans lequel il baigne. Or, ce dernier constitue tout autant un système que le premier.
Si nous avons jugé bon de distinguer les deux, c’est simplement pour pouvoir mettre l’accent sur ce qui nous intéresse principalement, à savoir le « système » (figure 1), et plus précisément l’analyse de ce « système » en détail. Pourtant, nous sommes tout à fait conscients qu’il existe certaines choses dans l’« environnement » environnant de la figure 1 qui sont importantes pour notre analyse. Néanmoins, celles-ci ne devraient pas être au centre de notre analyse. Nous avons décidé de ne pas analyser l’« environnement » de façon aussi détaillée que le « système ».
Nous pouvons dire que la théorie des systèmes a servi ici à tracer la frontière entre le « système » et l’« environnement ». Ce n’est pas anodin. Et nul doute que notre travail ne sera pas à point du premier coup. L’analyse des systèmes consiste alors à analyser ensuite la configuration et le comportement du « système », à condition d’avoir bien choisi des hypothèses sans doute brutes et simplificatrices au sujet de son « environnement ».
Mais, encore une fois, qui est aux commandes du « système » de la figure 1?
Un seul poste de commandement, mais quatre candidats rivalisant pour l’occuper
Nous avons déjà écrit auparavant qu’il y avait quatre stratégies d’affaires, chacune correspondant à quatre positions — points de vue ou attitudes — façonnées par l’expérience de quatre environnements de risque économique différents.[2] Nous avons défini quatre « périodes » de risque qui constituent le cycle d’affaires bien connu, soit les quatre « environnements de risque » de la figure 2. Chaque période de la figure 2 est associée à une attitude face au risque et à une stratégie de gestion du risque et dure souvent plusieurs années. Toutefois, il arrive que nous vivions des perturbations et des changements d’une période à l’autre et dans un intervalle de temps très court, comme pendant la pandémie.
Figure 2
Les quatre périodes et les quatre stratégies d’adaptabilité rationnelle en GRE
Quelle que soit la rapidité de ces changements qualitatifs importants dans l’environnement de risque d’une entreprise, nous avons plaidé en faveur d’un changement conséquent d’attitude face au risque et de stratégie du contrôle automatique, de la façon la plus rapide et la plus ordonnée qui soit, et nous avons appelé cela l’« adaptabilité rationnelle en GRE ».
La plus grande difficulté? L’adaptabilité rationnelle
Tant que la période de risque perdurera, immuable, le processus de base de contrôle automatique par rétroaction de la figure 1 fonctionnera sans anicroche, à condition que le bon pilote automatique — « bon » pour la période actuelle, pour être précis — soit aux commandes de la boîte de décision K. Toutefois, d’importantes difficultés apparaissent lorsque l’environnement de risque de la société change qualitativement en passant d’une période de risque à une autre.
Comment arriver à faire sortir un pilote automatique de la boîte de contrôle automatique K de la figure 1 et à le remplacer par un autre, compte tenu des trois possibilités de la figure 2? Autrement dit, comment faire pour remplacer la stratégie de décision que privilégie la société par une stratégie adaptée à la nouvelle période?
En guise de première réponse, nous avons déjà proposé un processus d’adaptabilité rationnelle pour réagir face à l’évolution des environnements de risque. Nous avons aujourd’hui un nom pour qualifier le spécialiste de ce processus : l’adaptateur.[3] L’adaptateur se fixe comme objectif de faire évoluer l’entreprise en fonction du changement environnemental en modifiant la stratégie de gestion du risque de la figure 2 pour mieux tenir compte du nouvel environnement.
L’un des moyens d’y parvenir a pour nom « système de contrôle automatique en cascade ». La figure 3, qui a été créée pour faciliter la prise de décision en matière de provisions techniques (boîte K) en fonction des portefeuilles d’actifs et de passifs de la société (boîte O), est un exemple de système de contrôle automatique en cascade.
Stratégie
Pour commencer, considérons la moitié inférieure du système de contrôle automatique en cascade de la figure 3 — son segment « stratégie », comme une sorte de « salle des machines » de la société d’assurances. Dans ce cas-ci, nous l’avons illustrée dans l’optique de la prise de décision en matière de provisions techniques, à savoir : quoi ajouter dans le portefeuille d’actifs, quoi enlever, dans le contexte de perturbations constantes du comportement des actifs. Ces perturbations, nous le soulignons, se trouvent très loin de la société d’assurances. Elles ont leur source dans l’« environnement de risque » qui entoure le « système » (figure 3), et leurs variations au fil du temps sont habituellement suivies au moyen d’indices comme le S&P 500. Par conséquent, dans le segment « stratégie », nous supposons l’existence de quatre versions possibles de la façon dont le contrôle automatique par rétroaction peut s’appliquer au choix de la décision à prendre en matière de provisions techniques. La société obtient donc l’excédent de trésorerie qu’elle souhaite, indépendamment de l’incertitude quant au comportement des actifs sur le marché.
Nous supposons pouvoir mettre l’une ou l’autre des quatre stratégies de décision de la figure 2 dans la boîte K du segment inférieur de la société de la figure 3, c.-à-d. l’une ou l’autre des quatre règles de contrôle automatique structurées différemment, ou quatre pilotes automatiques distincts. Au cours d’une période de risque donnée, et à ce niveau de la salle des machines, nous avons soit le maximaliste aux commandes, soit le directeur, le prudent ou le pragmatiste. Tant que la stratégie privilégiée — et si bien adaptée — porte ses fruits pendant la période de risque actuelle — autrement dit, le profil de risque associé au comportement des actifs du côté gauche de la figure 3 —, la société obtient essentiellement ce qu’elle veut et réussit parfaitement bien à cet égard.
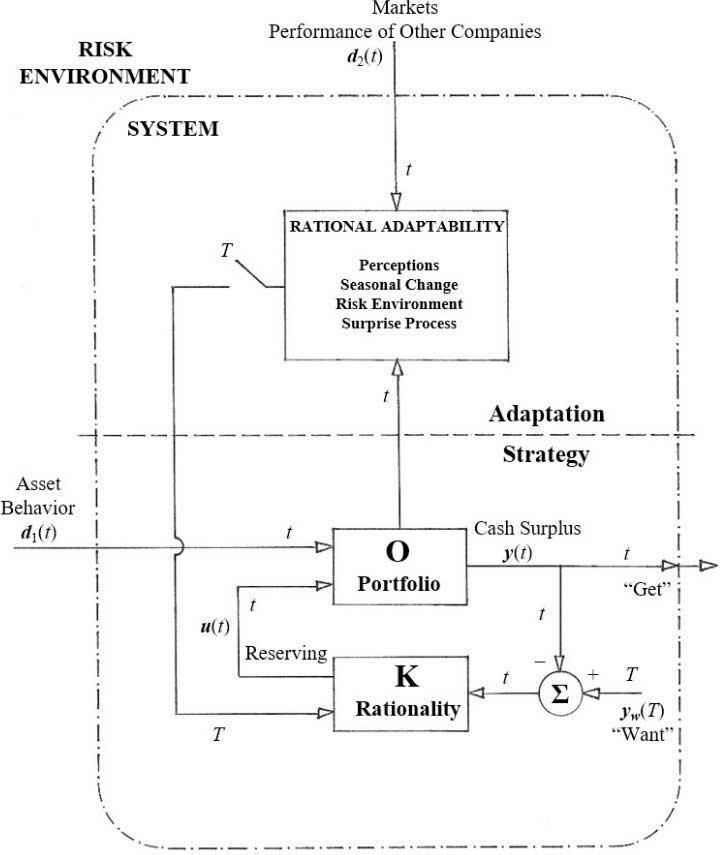
Figure 3
L’adaptation rationnelle sous forme de système de contrôle automatique en cascade aux fins de la prise de décision en matière de provisions techniques[4]
Le problème survient évidemment lorsqu’on a une des stratégies dans le bloc du contrôleur (maximisation, gestion des risques, prudence ou pragmatisme) et que la période de risque a changé. Que faire? Pour cela, il faut un changement qualitatif, soit un net écart, voire une perturbation, dans la cadence et les propriétés statistiques fondamentales des risques auxquels la société est exposée. Ces circonstances nous amènent au cœur de ce à quoi ressemble l’adaptabilité rationnelle en GRE dans le cadre de l’ingénierie du contrôle automatique.
Adaptation
Examinons maintenant le segment « Adaptation » dans la moitié supérieure du système de contrôle automatique en cascade de la figure 3. En fait, suivez la flèche sortant du segment inférieur « stratégie ». Symboliquement, il transmet de l’information opérationnelle sur tout ce qui passe dans le segment inférieur. La flèche atteint le bloc Adaptabilité rationnelle, à la manière d’un flux d’information au sujet d’autres éléments de l’« environnement de risque » de la société d’assurances, comme le comportement des concurrents sur les marchés de produits de la société. À la gauche du bloc Adaptabilité rationnelle, là où l’on voit un flux d’information sortant utile à la prise de décision, se trouve la représentation d’un commutateur selon l’ingénierie du contrôle automatique. Le commutateur est ouvert en ce moment.
Passons maintenant à l’étape cruciale de notre argumentation.
Nous insérons la notion d’adaptateur dans le bloc Adaptabilité rationnelle. Supposons que l’adaptateur détecte, d’une façon ou d’une autre, que la période de risque ne correspond plus à la stratégie de la société, étant déplacée, en l’état, dans la salle des machines du bloc du contrôleur en dessous (dans le segment « stratégie » de la figure 3). Supposons en outre que l’adaptateur a déterminé — encore une fois, d’une façon ou d’une autre—, la nouvelle période de risque et, par voie de conséquence, la nature du nouveau pilote automatique (maximaliste, directeur, prudent ou pragmatiste) qui est aux commandes de la boîte K de « stratégie ».
Nous devons examiner la figure 3 de plus près.
Évolution rapide et évolution lente
Lorsque nous examinons la figure 3 dans le détail, nous voyons que presque toutes les flèches (elles désignent les flux de risque, d’information ou de trésorerie) sont marquées de la minuscule t pour indiquer et souligner le microtemps, c’est-à-dire le fait que des choses évoluent assez rapidement au fil du temps et que des choses changent à court terme.
Seules deux des flèches — le très important signal de commutation du bloc supérieur Adaptabilité rationnelle et, d’une importance moindre pour les besoins actuels, la flèche « Want » — sont marquées de la majuscule T pour désigner le macrotemps, soit une évolution lente ou saisonnière des choses ou un changement à long terme. Par conséquent, nous devons faire ici une distinction entre ce qui se passe d’une période à l’autre, que nous représentons par la majuscule T, et ce qui se passe du point de vue des variations quotidiennes courantes des activités, que nous représentons par la minuscule t.[5] Il importe de faire remarquer que le commutateur à côté du bloc Adaptation rationnelle du système de contrôle automatique en cascade de la figure 3 ne se ferme qu’occasionnellement, quoiqu’en un « instant ». Bien que la commutation elle-même soit idéalisée, comme si elle se produisait de façon instantanée (« comme ça »), ces occasions sont relativement rares et éloignées les unes des autres. Elles sont alors marquées par des points dans le macrotemps T.
Eh bien, voilà l’idée générale, du moins en principe. Mais maintenant, avec la pandémie, l’activation du commutateur s’effectue en temps quasi réel. Par conséquent, T et t désignent presque la même chose. De très gros changements ou suppressions en matière de politique stratégique ont été mis en œuvre en peu de temps, pour seulement être ensuite mis en œuvre de nouveau.
Pourtant, même pour la prise de décision familière des entreprises, il y a un problème! Que faut-il faire, évidemment, à propos de ces deux et très gros « d’une façon ou d’une autre » susmentionnés? Que doit-on faire pour :
- déceler la nature de l’environnement de risque entourant la société, c.-à-d. déterminer la période de risque?
- sentir et détecter une transition imminente ou réelle dans cet environnement de risque?
- déceler la stratégie à privilégier pour faire face à la nouvelle période de risque postérieure à la transition?
Première réponse : considérer la surprise comme un “ mégadécalage ”
Dans nos travaux antérieurs sur l’adaptation rationnelle en GRE, et en l’absence de tout ce qui pourrait ressembler à la figure 3, le commutateur de l’adaptateur a été tiré selon une typologie de « surprises », et les surprises, notons-le, ont tout à voir avec l’apprentissage organisationnel dans ce contexte[6]
Il est utile de commencer par tracer un parallèle. Ce que le « décalage » du contrôle automatique de base par rétroaction représente pour la « stratégie » d’exploitation courante de la figure 1 correspond à ce que la « surprise » du contrôle automatique en cascade représente pour la fonction de commutation de l’adaptabilité rationnelle dans le segment supérieur « adaptation » de la figure 3.
Mais ici s’arrête la similarité. Pour dire les choses simplement, nous devrions considérer la « surprise » comme un « mégadécalage ». Dans l’ensemble, il s’agit d’une dissonance fondamentale, propre à ébranler les croyances, entre la façon dont le pilote automatique aux commandes de la boîte K du segment « stratégie » de la figure 3 considère le monde et la façon dont le monde est réellement. Au niveau plus prosaïque des détails techniques courants — en bas dans la salle des machines du segment inférieur de la figure 3 (et en se focalisant sur ce qu’on appelle la jonction de comparaison, soit le petit cercle comportant le symbole de sommation Σ) — il s’agit d’un « décalage » persistant entre les résultats réels et les objectifs. Pourtant, cette dissonance technique est niée par la personne qui est aux commandes. Jusqu’à ce que, en vérité, étant persistante, elle augmente… et augmente… et augmente… jusqu’à… « surprise »!
Ainsi, selon notre façon première et antérieure de gérer l’adaptation rationnelle, une telle « surprise » est le cœur même du problème. C’est là que le « monde construit » et entièrement prévu de l’un ou l’autre des quatre pilotes automatiques aux commandes de la boîte K de la « stratégie » est confronté au « monde unique de la réalité » que nous tous habitons, sans égard à nos croyances fondamentales quant aux risques. La « surprise », quand (si) elle finit par se manifester — lorsqu’elle se manifeste chez le pilote automatique aux commandes et que la société d’assurances navigue dans des conditions atmosphériques assez différentes de ce qu’elle avait supposé et qui dureront à jamais (et de façon incontestable, comme un acte de foi) —, est une version « méga » du « décalage » quotidien du contrôle automatique par rétroaction de la figure 1. Qui plus est, ce « mégadécalage » ne peut être corrigé par une mise au point quotidienne.
La surprise doit être suffisamment choquante pour provoquer l’apprentissage et pour ébranler les convictions fondamentales relatives à chacune des quatre attitudes face au risque de la figure 2. Quelqu’un doit tirer le commutateur à côté du bloc Adaptation rationnelle dans le haut de la figure 3.
Expériences de surprise empiriques
La typologie de « surprises » est l’un des moyens de déterminer la façon exacte de tirer le commutateur. Plus prosaïquement, il s’agit d’une typologie des différents éléments de preuve empiriques (non quantitatifs) de ce que vit chacun des quatre partisans de la « stratégie » lorsqu’il est (éventuellement) surpris de réaliser que la période de risque n’est pas du tout celle pour laquelle la stratégie avait été conçue. Chacune des quatre stratégies peut subir trois surprises de ce genre. Par exemple, il y aura trois occasions où le directeur — qui est très à l’aise lorsque la période de risque est modérée — devra être surpris et complètement secoué au moment de prendre des décisions. De telles situations se produiront lorsque le pilote se rendra finalement compte qu’une période de risque, caractérisée par une expansion, une récession ou l’incertitude, est « imminente ».
La figure 2 montre les quatre stratégies, chacune adaptée à l’un des quatre environnements de risque. À tout moment, l’une des quatre stratégies sera active, sise au niveau inférieur de la boîte K de la figure 3. Laissé sans surveillance, chaque pilote automatique finira par ne plus être en accord avec la période de risque qui évoluera inexorablement et finira par changer. Le contexte commercial actuel aura évolué.
Un jour ou l’autre (encore une fois), il y aura une « surprise ». Chacune des quatre attitudes face au risque peut être invoquée pour son expérience de la performance de la société d’assurances par rapport aux perceptions de la réalité. Parmi les 12 catégories de « surprise », il y aura des expériences sommaires telles que :
- « L’espérance de bonnes aubaines de temps à autre est vaine — ce n’est que perte après perte après perte », dit le pragmatiste en signe de protestation lorsqu’il est confronté à une récession (par opposition à un environnement de risque caractérisé par l’incertitude).
- « Un effondrement total », s’emporte le maximaliste après l’entrée en récession.
- « Des périodes inattendues de bonne ou de mauvaise chance se sont produites », dit le pragmatiste d’un air songeur lorsqu’il est surpris d’entendre le pilote parler de la période de risque modéré.
- « D’autres prospèrent sans faire preuve de prudence », déplore le prudent lorsque la période est caractérisée par un risque modéré ou une expansion.
Et ainsi de suite.
Étant donné qu’il n’y a jamais qu’un seul monde de réalité et quatre mondes construits, les rapports d’expériences empiriques comme ceux qui précèdent vont toujours comporter un monde réel et trois mondes qui sont faux. En effet, l’abondance des gémissements, des grognements et des plaintes jalouses qu’il ne faut pas sous-estimer découle de la pluralité des quatre voix de la société, pourvu que leur viabilité ait été préservée et entretenue par la société (ce point sera abordé à la partie II du présent article).
Mais laquelle des quatre voix va tomber dans le mille et prendre comme il se doit les commandes de la stratégie de la société dans la boîte K? Car chacune d’entre elles s’entêtera à dire qu’elle a la bonne réponse, y compris celle qui a réellement visé juste et qui est sans doute souriante et affiche peut-être un air suffisant[7].
Par exemple, après la crise financière de 2007, ce que nous avons appelé une période d’incertitude quant au risque a prévalu pendant plusieurs années. Elle correspondait très bien à la stratégie de gestion du risque du pragmatiste de la figure 2. Pourtant, certaines sociétés d’assurances se sont accrochées à la stratégie du prudent, convaincues que toute période d’incertitude n’était qu’une simple pause momentanée (dans l’environnement de récession de 2008-2009) avant que la récession ne s’installe à nouveau.
À notre connaissance, cependant, les typologies de « surprises » ne font pas partie des éléments constituants des boucles de contrôle automatique par rétroaction. Alors, comment l’adaptateur s’y prendra-t-il pour déterminer l’existence d’un changement dans la période de risque ou d’un changement qualitatif dans la stratégie et le succès apparents de la société? Par-dessus tout, nous devrions souhaiter que l’adaptateur en arrive à un diagnostic définitif et tire le commutateur de la figure 3, et mieux vaut tôt que tard. Et plus rapidement sans doute que l’éternité apparente qu’il puisse falloir pour que l’un ou l’autre des quatre pilotes automatiques soit choqué de se rendre compte à quel point sa stratégie de gestion du risque est inappropriée — et quitte les commandes! Parce que tant que la période de risque sera toujours ce que le groupe « stratégie » aux commandes croit qu’elle est, le groupe s’entêtera à dire qu’il est inutile de changer quoi que ce soit.
À cette fin — soit d’accélérer le diagnostic définitif —, nous offrons à l’adaptateur des modèles hypothétiques avec lesquels il peut travailler.
Seconde réponse : l’ingénierie du contrôle automatique et ses modèles
Dans notre seconde réponse, nous abordons donc le diagnostic de la typologie des « surprises » et la fonction de commutation de l’adaptateur par la substitution de modèles, mais de modèles comportant un ingrédient spécial d’ingénierie du contrôle automatique.
Au lieu de solliciter les vues des pilotes automatiques qui se rivalisent et qui sont peut-être même surpris, nous supposons que divers flux de données formelles (séries chronologiques) deviennent accessibles à l’adaptateur et s’accumulent jour après jour :
- des flux de données, comme on peut s’y attendre, liés à l’évolution de l’« environnement de risque » de la figure 3, comme les valeurs d’actifs suivies par divers indices (le d1 qui influe sur la « stratégie ») et les comportements des concurrents et de leurs produits sur le marché (le d2);
- des flux de données provenant du « système » de la figure 3, selon le modèle de prise de décision opérationnelle de la société d’assurances, tel qu’il émerge de la boîte de contrôleur K (le u de la figure 3), et le suivi des données sur sa performance (le y).
Compte tenu de ces séries chronologiques, nous supposons que divers modèles de type économétrique d’entrée-sortie ou à une seule variable peuvent être utilisés pour l’analyse de l’évolution de l’environnement de risque de la société et de sa performance face à cet environnement, notamment en ce qui concerne la nature de sa prise de décision (dans la boîte K de la figure 3). Il s’agit des modèles en temps discret de l’ingénierie du contrôle automatique (tout comme ceux utilisés par Balzer et Benjamin). Chacun de ces modèles peut faire l’objet d’un rapprochement continu avec les données opérationnelles qui s’accumulent. Chaque modèle contient un ensemble de paramètres, ses coefficients. Voici donc la chose spéciale appartenant à l’ingénierie du contrôle automatique : nous transformons les paramètres de modèle en variables temporelles.
L’ingrédient spécial : des paramètres de modèle variables dans le temps
Nos modèles sont considérés comme les plus simples, ils sont donc erronés. Toutefois, il est possible de les rendre justes au moment de la prise de décision (en microtemps t) en leur appliquant des paramètres qui sont censés varier en fonction du macrotemps T.
De plus, ces paramètres seront jugés suffisamment importants en soi pour avoir leur propre symbole explicite α. Il ne s’agit pas de simples variables utiles au bon fonctionnement des variables plus importantes, , à savoir le d(t), le u(t) et le y(t). Elles concernent la structure des choses : ce qui est lié à quoi (parmi le d(t), le u(t) et le y(t)), de quelle façon et par quel mécanisme causal. Autrement dit, elles concernent la constitution ou la conception d’un système. Ce sont les paramètres variables dans le temps désignés par α(T).
Seul le symbole lui même, le α(T), occupera une place dominante dans la partie II du présent article. Il est synonyme d’espace paramétrique du système.
En préparation de la partie II du présent article : le « caractère exceptionnel » de l’adaptateur
Un air particulier d’exception se rattache à l’adaptateur : quelque chose qui tient de l’altérité, quelque chose à part entière. C’est tout à fait intentionnel. Notre adaptateur doit être façonné d’après l’archétype de l’ermite : la cinquième rationalité de la théorie culturelle de l’anthropologie sociale, qui est la théorie qui a façonné l’adaptabilité rationnelle en GRE jusqu’à présent, mais qui n’utilise que les quatre rationalités de base.
Ainsi, quel que soit ce dont chacune des quatre autres attitudes (rationalités) de la figure 2 tient compte (à sa manière) — parmi le d(t), l’u(t) et le y(t) — nous allons faire en sorte que notre adaptateur concentre plutôt son attention sur α(T). Ce faisant, nous attribuons une grande importance au rôle des données sur α(T) dans les travaux complémentaires de diagnostic « surprise » de l’adaptateur, et cette importance dépasse celle du d(t), de l’u(t) et du y(t).
Mais il y a plus à l’espace paramétrique de α(T) — beaucoup plus, et plus au caractère exceptionnel de l’adaptateur — que l’utilisation diagnostique de α(T) pour soutenir la fonction de commutation de l’adaptateur. Ce supplément est lié à ce que nous appelons la fonction de développement de l’adaptateur. Il renvoie à une considération plus importante, à savoir comment développer le corps du système — son tissu ou sa structure — afin qu’il puisse fonctionner avec résilience. Il faudra pour ce faire investir continuellement dans les ressources humaines, financières et matérielles de la société d’assurances. Sa présentation et son analyse font l’objet de la partie II du présent article.
Nous verrons que l’essentiel de cette propriété systémique de résilience peut être déduit du mode d’organisation des écosystèmes naturels. Dans ce corps organisationnel résidera la capacité d’une société d’assurances à accomplir les deux tâches suivantes : tout d’abord, naviguer avec aplomb à travers toutes les périodes de risque et au-delà dans un avenir encore plus lointain; ensuite, améliorer les perspectives de la société en restructurant sa composition avec succès, notamment dans les conditions de ce que l’économiste Schumpeter qualifierait de « destruction créative ».
En d’autres termes, le développement, par l’adaptateur, du corps de la société devrait permettre à celle-ci d’afficher non seulement le « rebond » caractéristique de la résilience, mais aussi un « rebond en avant », comme l’ont exprimé certains économistes (encore). La meilleure illustration pratique de ce qui s’apparente à un développement par l’adaptateur est la surveillance des ressources humaines réparties entre les entreprises en démarrage situées sur le campus d’un écosystème d’innovation à Linz, en Autriche. Cette étude de cas sera présentée à la partie II.
Un lien pour se rendre jusqu’à l’espace paramétrique de α(T)
Il n’est pas facile de pénétrer la « façon de voir les choses » de l’espace paramétrique de α(T). Nul doute non plus qu’une pensée aussi étrange ne se retrouve pas chez beaucoup de gens. Toutefois, il est essentiel d’explorer à fond ce que la résilience pourrait représenter. Voici un lien qui vous amènera à un document supplémentaire comportant une discussion et une élaboration beaucoup plus approfondies de la pensée systémique qui relie logiquement les parties I et II de cet article.
Toutefois, la lecture et l’assimilation du contenu du lien ne sont pas une condition préalable à la lecture de la partie II, lorsque la suite de cet article paraîtra dans le prochain numéro de ce magazine. Mais encore une fois, tout a été fait dans ce document pour faciliter la montée dans un espace paramétrique. Dans la mesure du possible, notre discussion à ce sujet est liée à des sujets plus connus, en particulier l’économie, mais aussi l’écologie (en tant qu’origine de la résilience) et l’anthropologie sociale (comme fondement théorique de l’adaptabilité rationnelle en GRE). Toutefois, il sera davantage question de l’ingénierie du contrôle automatique. En ce sens, le lien est une invitation à un exercice de « pensée systémique » interdisciplinaire, tout comme la présente partie I et la prochaine partie II de notre article.
Alors, en peu de mots, qu’est ce qu’il y a pour nous dans ce document accessible par lien?
Le document s’écarte de l’ingénierie du contrôle automatique de missiles guidés et se termine par un retour au problème de la fixation des primes de Benjamin et Balzer, par lequel nous avons commencé la présente partie de notre article. En résumé, on peut se retrouver avec quelque chose de vraiment très sophistiqué — en matière d’apprentissage et de contrôle automatique tout à la fois et en même temps — et qui mériterait d’être qualifié de « super magique » dans la boucle de rétroaction de la figure 1 ou de la figure 3. Les ingénieurs automaticiens appelleraient cela le double contrôle automatique adaptatif. Il tire notamment son origine des systèmes de guidage de missiles.
En cours de route, une distinction ferme est établie entre les propriétés systémiques de stabilité à court terme et la résilience à long terme. C’est ce qui nous amène au cœur de l’espace paramétrique de α(T) — et même de l’imagerie d’animation image par image.
Nous abordons aussi les points suivants. Si le α(T) figure explicitement dans un modèle de stratégie de décision dans la boîte de contrôleur K de la figure 1, il permet d’avoir une règle de décision dont la structure est unique pour parcourir le cycle (au fil du temps T) à travers les quatre « pôles » archétypes que sont le maximaliste, le directeur, le prudent et le pragmatiste (figure 2). La quadruple diversité de la prise de décision en microtemps t est obtenue approximativement par la substitution d’une règle décisionnelle unique dont la structure (ses paramètres α) varie au fil du macrotemps T, d’où la variabilité de la stratégie de décision.
La modélisation de la diversité de la prise de décision plutôt que la modélisation de la variabilité de la prise de décision est notamment le titre de notre récent rapport de recherche de la SOA (2021), sur lequel repose le présent article. Il faut toutefois dire que la partie II et le document accessible par lien vont bien au-delà du contenu du rapport de recherche.
Les faits énoncés et les opinions formulées dans le présent document sont ceux de chaque auteur et ne correspondent pas nécessairement à ceux de la Society of Actuaries, des rédacteurs du magazine ou des employeurs des auteurs respectifs.
M. Bruce Beck, Ph. D., est chercheur en résidence auprès du cabinet FASresearch, à Vienne, et chercheur principal invité auprès de l’International Institute for Applied Systems Analysis (IIASA). On peut le joindre à mbrucebeck@gmail.com.
David Ingram, FSA, CERA, FRM, PRM, est consultant à temps partiel auprès de la société Actuarial Risk Management et chercheur, rédacteur et conférencier indépendant en matière de GRE et d’assureurs. On peut le joindre à dingramerm@gmail.com.
Michael Thompson, Ph. D., est chercheur émérite auprès de l’International Institute for Applied Systems Analysis (IIASA). On peut le joindre à michaelthompsonbath@gmail.com.