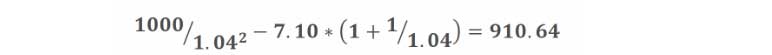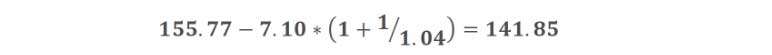Behavioral Economics and the Longevity Problem
By Craig W. Reynolds
Risk Management, February 2023

Fear of outliving retirement savings is common for retirees or those facing the decision of when to retire. This fear is exacerbated by the continuing decline of defined benefit (DB) pension plans. According to the Congressional Research Service, only about 10 million active American workers are covered by defined benefit pension plans, down from around 30 million in the early 1980s. [1]
The insurance industry is uniquely positioned to fill the gap left by the decline of such plans, primarily utilizing payout annuities, including deferred income annuities and guaranteed lifetime withdrawal benefits (GLWB) on indexed or variable deferred annuities. Yet market penetration for these products is relatively low.
Why don’t more people buy annuities? Many reasons are commonly cited, including:
- Lack of understanding of longevity risk;
- lack of awareness or understanding of annuities;
- asset concentration or liquidity concerns;
- perceived to be expensive;
- tax-deferred but, unlike life insurance, not tax-free;
- no trigger events such as marriage, birth of children, or home purchase to motivate purchase; and
- concern that insurers may not be able to deliver on their promises.
However, the classic behavioral economics research of Daniel Kahneman and Amos Tversky in prospect theory may provide insight into why annuities are not as popular as life insurance. More importantly, prospect theory might provide clues as to how to design and market annuity products to make them more attractive to consumers.
In this paper we provide an overview of Kahneman and Tversky’s theory, postulate how their work might apply to life insurance and annuities, and use the insights gained to suggest a new product concept that could be the breakthrough product insurers need to enter the longevity insurance market in a new and successful way.
Prospect Theory
Prospect theory is, at its core, an explanation of how people evaluate risk. It explains why people sometimes make what appear to be irrational or inconsistent decisions depending on how their choices are framed. Kahneman and Tversky pioneered work in this field in the 1970s, leading to a Nobel Prize for Kahneman in 2002. (Tversky died in 1996.)
Unlike prior models of decision making, in which the decision maker is assumed to be fully rational and utility-maximizing (e.g., Von Neumann & Morgenstern[2]), Kahneman and Tversky demonstrated that people weigh gains and losses quite differently, and alter their decisions accordingly, depending on whether they see a decision outcome as a gain or a loss. As a result, people can switch their preferences for risk simply by how the outcome of a decision is framed—whether something is gained or lost influences its perceived value, and losses loom larger than gains. In other words, the prospect of a loss hurts more than the pleasure of an anticipated gain of a similar magnitude. Across multiple decades of research, decision makers have been shown to shift their preferences in the direction of loss avoidance, even if that means adopting a position of risk—even without compensation for doing so. These “preference reversals” violate a central tenet of traditional, economic models of decision making, in which a decision maker is assumed to be fully rational.
This is more than an issue of a nonlinear utility function. When faced with a decision, the choices that individuals make will tend to change with the framing of the question, even if the underlying economics are not changing.
A simple pair of choices illustrates the concept of preference reversal, which is a key experiment in prospect theory.
Suppose that 600 people are expected to die of the flu. Two treatment options are available.
- Treatment A will save 200 people with 100 percent certainty.
- Treatment B will save everyone with a one-third chance and no one with a two-thirds chance.
Kahneman and Tversky’s seminal research[3] showed that 72 percent of their sample would choose Treatment A. This is interesting in and of itself, because these options are in some sense equivalent, as they have the same expected value. Each treatment has an expected value of 200 people being saved. However, in this scenario, most decision makers preferred the certainty of saving at least some of the lives.
Now consider an alternative way to present the same treatment options:
- If Treatment C is used, 400 people will die.
- If Treatment D is used, there is a one-third chance that no one dies and a two-thirds chance that everyone dies.
Their research showed that 78 percent will choose Treatment D over Treatment C in this choice presentation. In this case, decision makers choose the gamble despite the potential loss of all lives. Unlike in the first scenario, where they preferred the certainty of saving lives, in the second they preferred the option that offered the possibility that no one might die.
This is a simple example of preference reversal. In all scenarios, the expected outcome of the decision (the expected value of the number of people saved versus the number of people who die) is the same. What changes is whether the decision is a gamble versus a sure thing, and whether the decision is framed as a loss (people will die) or a gain (people will be saved):
- Treatments A and C (the sure things) both result in 200 people living and 400 people dying.
- Treatments B and D (the risky options) both have a two-thirds chance of everyone dying and no one living, with a one-third chance of everyone living and no one dying.
A = C and B = D, and around three-quarters of people polled prefer A to B, so rationally around three-quarters should prefer C to D. Yet around three-quarters prefer D to C. Why do we see this apparently inconsistent result?
Kahneman and Tversky’s generalization of this phenomenon is that individuals are “risk averse in the domain of gains and risk seeking in the domain of losses.” In other words, when talking about cures (a gain), most people choose the sure thing rather than the uncertain outcome with the same expected value. When talking about deaths (a loss), most of us are willing to roll the dice to try to avoid a bad outcome.
Prospect Theory in Life Insurance and Annuities
Though Kahneman and Tversky did not, to the best of my knowledge, apply their work to life insurance and annuities, similar principles may apply here. This concept has been explored by other researchers who postulated more effective ways to sell annuities by adjusting the framing.[4] This paper expands upon that work to analyze annuities and life insurance from a financial gain and loss perspective.
One can argue that life insurance is most often sold in the domain of losses, while annuities are most often sold in the domain of gains.
While life insurance can be, and sometimes is, sold as an investment, most potential customers are likely thinking primarily about the risk of death, and insuring against that risk. It is hard to think of something much more obviously in the domain of losses than the discussion of death.
In contrast, annuity products are likely most often sold as investments. Presentations of retirement income are clearly in the domain of gains. While one can sell these products as insurance against longevity, it is hard to think about unexpected longevity as a loss, even though it is one from a financial perspective.
Kahneman and Tversky’s prospect theory would thus suggest that people will be risk-seeking when considering life insurance, and risk-averse when considering annuities. Is this consistent with reality, where more people own life insurance than annuities? Fifty-two percent of American consumers own life insurance,[5] whereas only 12 percent own annuities.[6]
Interestingly, at first this may not seem to be the case, because we often think of life insurance as insuring against a risk. It seems like it is reducing risk. But as a standalone transaction, its financial return is very uncertain.
If a potential insured does not buy life insurance, and instead deposits $1,000 in the bank, leaving it there, then at death the heirs will get the accumulated value of that $1,000. The present value (PV) today of the accumulated balance is $1,000, if discounting at the after-tax earned rate. Ignoring for now the risk of bank default, the gain (loss) on the savings account transaction is absolutely certain to be zero.
If the individual does buy life insurance, assuming no profit or expense loads for the sake of simplicity, the expected present value of the transaction is zero, so we are back in the first case. But the actual resulting present value of the transaction has high uncertainty, with large financial gains for the policy owner for early death, and small financial losses for late death.
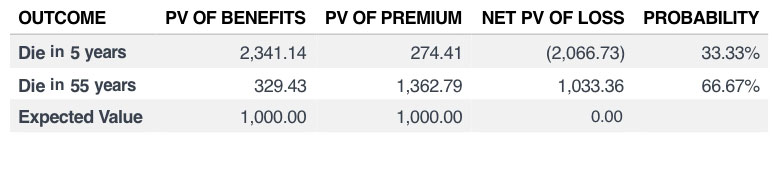
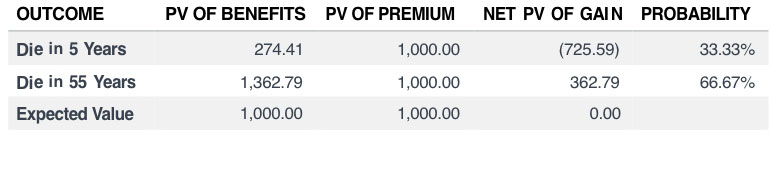
Consider a very simple example with a whole life product reflecting no loads or profit. Further assume a 4 percent discount rate, and that the policy is issued to an insured with a one-third chance of dying after five years and a two-thirds chance of dying after 55 years. Using some simple actuarial math, one can show that a single premium investment of $1,000 (or a level annual premium of $59.27) would buy a whole life face amount of $2,848.36. Alternatively, this $1,000 could buy a single premium immediate annuity (SPIA) with an annual payment of $59.27. Which product is riskier, the level premium whole life or the SPIA?
Figure 1
Simplified Life Policy Outcomes
Figure 2
Simplified Annuity Policy Outcomes
By construction, because we assume the mortality rate distribution is known and certain and there are no loads or profit, both the annuity and the whole life purchase have an identical expected gain of zero. But the net loss for the life policy (to the policy owner) has much more volatility associated with it than does the annuity policy. In fact, the standard deviation of the net loss on the life policy, $1,461, is almost three times that of the annuity policy, $513.
But now think about the purchase decision. As discussed earlier, the life policy purchaser is in the domain of losses. Accordingly, the purchaser is risk-seeking, as compared to the no-purchase scenario, where no loss is locked in. The life policy purchasers are willing to take on risk because they are in the domain of losses.
For the annuity purchaser, who is in the domain of gains, the purchase of a risky investment, even though less risky than the life policy, is not attractive.
A Slightly More Realistic Example
We can make the example a little more realistic to better understand the risk profile. We will continue to consider a guaranteed product with a 4 percent interest rate and no expense or profit loads, but now we utilize mortality equal to the 2015 Valuation Basic Table (VBT) for a 35-year-old male nonsmoker. What does the risk profile look like then?
Here two streams of payments of $7.10 (premiums in the case of the whole life policy, and annuity payments for the SPIA) both have a present value equal to $155.77, which is equal to the net single premium for a whole life policy with a face of $1,000. Given this policy data, we can show the risk profile as a function of time until death. As an example, if the policyholder dies in year two, the gain in the life policy is:
The comparable loss on the annuity policy is:
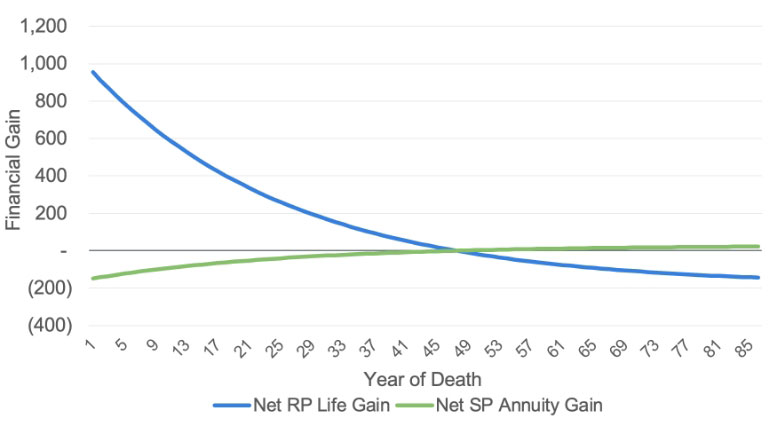
Figure 3 illustrates how these losses compare for all possible years of death
Figure 3
Policyholder Gain on No-load SPIA or Whole Life as a Function of Year of Death
From Figure 3, we can make a few relevant and interesting observations:
- The life product has a hugely positive financial return for early death, and a modest loss for late death.
- The annuity product has a modest loss for early death and a modest gain for late death.
- Both products have risk (uncertain returns), but the life product clearly has a wider dispersion of possible outcomes.
In summary, the outcomes can be recapped as in Figure 4.
Figure 4
Annuity/Life Financial Outcome Recap
Perhaps we can find a way to combine these products in a way that ameliorates the bad scenarios by dampening some of the very good scenarios. Would such a product be easier to sell?
A Potential Hybrid Solution
If a customer needs to be a risk-seeker to purchase an annuity product, because annuities are perceived to be in the domain of gains, we have two possible solutions to the annuity sales problem:
- Market annuities in such a way as to emphasize the longevity risk more than the investment potential, in hopes of reframing the decision as being in the domain of losses.
- Wrap the annuity inside a life product to allow it to piggyback on the domain of losses framing of the life product.
The first scenario is always going to be hard. How can an agent convince a prospect that living a long time is a bad outcome? Yes of course it is a bad financial outcome, but it is wrapped up with the idea of a long life. Thus, while this may be an effective sales strategy, it may be challenging to successfully implement.
Let’s instead consider the second possibility. What would happen if we wrapped an annuity inside a life insurance policy? Specifically, let’s design a universal life (UL) insurance policy rider that adds a cost-of-longevity deduction to the usual cost of insurance deduction to purchase layers of deferred income annuities (DIAs).[7] This solution combines protection for the risk of dying “too soon” with protection for the risk of dying “too late.”
DIAs are a cost-effective way to manage longevity risk. The flexible nature of UL would allow policyholders to decide how much of their policy risk charges will go toward buying normal mortality insurance, and how much will go toward buying longevity insurance. Specifically, in the early years of the life insurance contract, when mortality charges are rarely significant, the policyholder might elect to devote additional deductions to prefunding deferred retirement income at a time when the cost of doing so is comparatively low. By combining the longevity risk and mortality risk products together, the insurer benefits from economies of scale and can pass this savings on to create a more attractive product.
Specifically, we propose a product that would work as follows:
Design concept:
- DIA premiums are paid with a deduction from the UL account value.
- Each deduction buys a layer of DIA benefit.
- DIA purchase rates are subject to change but locked in for each layer once purchased.
- Policyholder specifies the schedule of DIA purchase payments (subject to change) as one of the following:
- A percentage of base mortality cost of insurance (COI),
- a per policy amount, and
- the excess of some late duration COI over current COI.
- Policyholder specifies DIA benefit start age in advance—each purchase locked in once made.
- DIA benefit has no cash surrender value, thus reducing Section 7702 compliance challenges.[8] The DIA benefit is the nonforfeiture benefit.
- Accrued DIA benefit persists even if UL policy lapses.[9]
From the insurer perspective, a product like this is more attractive than the sale of a standalone DIA because:
- Natural add-on sale to UL, especially for high-income customers,
- lower marginal administrative cost,
- mortality closer to life mortality than annuity mortality,
- automatic purchases spread over time at policyholder-defined and adjustable schedule,
- return versus year of death risk curve readily adjustable via changes to level of benefit purchases, and
- overcomes domain of gains risk aversion.
And it is better than a standalone UL product as well:
- Possible improved persistency,
- possible increased sales,
- mortality closer to annuity mortality than standard life mortality,
- natural mortality hedge, and
- increased assets under management.
The mortality issue is particularly noteworthy:
- One key contributor to the cost of DIA is the anti-selection effect. People in poor health will rarely buy DIAs, because they do not expect to live long enough to benefit from them. This makes annuities more expensive than they otherwise would be.
- People in very good health might be less prone to buy life insurance, because they do not expect to die soon. This makes life insurance more expensive than it otherwise would be.
By combining these products together, the DIA mortality will likely be higher than it would be for a standalone DIA product, and the life insurance mortality will likely be lower than it would be for a standalone UL product. This makes both products more competitive (or more profitable) than they otherwise would be. This is similar to the effect seen for life/long-term care (LTC) hybrid products.
How Costly is the DIA Benefit?
The cost of the benefit will depend on the specifics of the policy design. We created a generic model of the DIA added to a simple current assumption UL policy based on the following key DIA-related assumptions:
- DIA cost of longevity deduction equal to a level amount up to the date of DIA benefit payments.
- DIA annual income equal to 5 percent of the life insurance policy face amount.
- 4 percent earned rate.
- VBT 2015 experience mortality.
- DIA benefits determined based on purchase rates consistent with:
- 2012 Individual Annuity Mortality (IAM) table mortality with G2 improvement,
- 2.75 percent earned rate, and
- no explicit expense or profit charges.
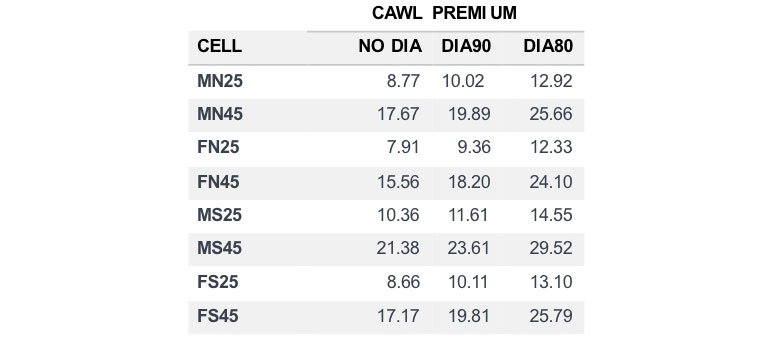
With the assumptions selected for this demonstration, the best estimate overall product after-tax and cost of capital internal rate of return (IRR) ends up in the range of 11 percent to 12 percent, irrespective of whether the DIA benefit is elected or not. Figure 5 recaps the annual current assumption whole life premium required to mature the policy for various ages and risk classes, without the DIA and for DIA benefits beginning at age 80 or 90. Of course, actual premiums would vary with product design, parameterization, funding pattern, and other assumptions. But Figure 5 gives an indicative feel of the cost of providing such coverage.
Figure 5
Impact of DIA on Required Premium
Conclusion
Would a product like this be right for every company and every consumer? Not likely. But packaging longevity protection with a domain of losses products like a UL, indexed UL (IUL), or variable UL (VUL) offers the potential for cross-selling that likely exceeds that of standalone products. And by bundling the DIA product together with the UL product, we can hope to circumvent the natural barriers to sales that were analyzed by Kahneman and Tversky, while simultaneously making both products more competitive than they would be on a standalone basis.
More work remains to be done to finalize design and pricing for any given company. More consideration would need to be given to asset-liability management strategy, commissions, assumptions, and risk management. But the work presented here presents a concept that might provide first-mover advantages for a company willing to explore this market.
Statements of fact and opinions expressed herein are those of the individual authors and are not necessarily those of the Society of Actuaries, the newsletter editors, or the respective authors’ employers.
Craig W. Reynolds, FSA, MAAA, is principal and consulting actuary for Milliman. Craig can be contacted at craig.reynolds@milliman.com.