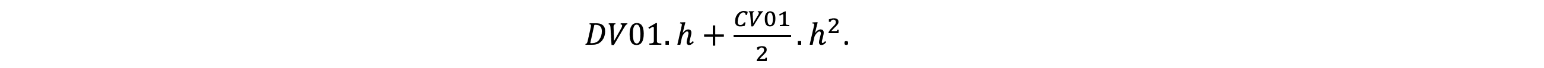Défis relatifs à la gestion du risque de taux d’intérêt : Partie 1 — Comment tirer le meilleur parti de l’actif et du passif d’une société
par Dariush Akhtari
Gestion du risque, février 2024

L’asymétrie de l’incidence des taux d’intérêt sur la valeur de l’actif et du passif pourrait nuire sensiblement aux bénéfices et à l’excédent des sociétés. Afin de quantifier et d’atténuer l’effet de cette asymétrie, les sociétés ont apparié une combinaison de duration et de convexité. Dans la présente partie de ce document à plusieurs volets, je passerai en revue ces techniques de mesure et leurs limites. Dans la prochaine partie, je proposerai une approche permettant de mieux comprendre à quel point on pourrait recourir à ces mesures et en accroître l’utilisation.
Pour atténuer le risque de taux d’intérêt, il est impératif d’apparier les caractéristiques de l’actif et celles du passif. L’asymétrie entre l’incidence des taux d’intérêt sur la valeur de l’actif et du passif peut nuire sensiblement aux bénéfices et à l’excédent des sociétés. À titre d’exemple, mentionnons le premier trimestre de 2020, où la courbe des taux au comptant a chuté de 138 à 87 points de base (pb) (entre la première et la 30e année). Pour quantifier et tenter d’en atténuer l’incidence sur l’excédent, il faut compter sur des modèles bien conçus qui projettent les flux de trésorerie de l’actif et du passif. Auparavant, on y parvenait en appariant la duration, ou en appariant la duration et la convexité de l’actif à celles du passif. Toutefois, ces techniques ne conviennent que pour immuniser le risque de taux d’intérêt contre des mouvements de faible envergure et parallèles. Dans la présente partie, j’utiliserai un exemple simple pour souligner que même avec une variation parallèle des taux, ces mesures comportent des limites. Dans la seconde partie de la présente série d’articles, je proposerai une méthode pour déterminer la fourchette de variations de taux pour lesquelles ces mesures de la gestion de l’actif-passif (GAP) peuvent être utilisées, la fourchette de « validité », à l’extérieur de laquelle un nouveau calcul des mesures de la GAP peut être nécessaire en plus de la nécessité éventuelle de rééquilibrer le portefeuille. De plus, dans cette seconde partie, je recourrai à une technique pour améliorer l’approximation de la variation de la valeur hors de la « fourchette de validité » susmentionnée.
Examen des diverses techniques de mesure et de leurs limites
De nombreux intervenants connaissent bien la duration et la convexité des mesures de la GAP. Toutefois, pour atténuer le risque d’incidence sur l’excédent (la valeur de l’actif réduite de la valeur du passif) après un changement de taux en appariant la duration et la convexité de l’actif et du passif, la valeur de l’actif doit être égale à la valeur du passif. Ce point peut être négligé à plusieurs égards, mais il est crucial. Une solution à ce problème consiste à faire correspondre la « valeur actualisée » ou la « valeur en dollars », la VA01, et la « valeur de convexité en dollars » d’un point de base, la VC01, de l’actif et du passif.
La VA01 désigne la valeur actualisée ou de la valeur en dollars d’une augmentation de 1 pb de la courbe des taux d’intérêt. Elle correspond à la valeur négative du produit de la duration et de la valeur marchande de l’instrument, divisée par 10 000. La VC01 représente la convexité en dollars de l’instrument pour une variation de 1 pb de la courbe des taux d’intérêt. Elle équivaut au produit de la convexité et de la valeur marchande de l’instrument, divisé par 100 000 000. Il est avantageux d’apparier la VA01 et la VC01 de l’actif et du passif, car il n’est pas nécessaire d’inclure que la restriction de valeur de l’actif soit égale à celle du passif. La variation de la valeur de l’instrument pour un déplacement parallèle d’un point de base de h correspondrait alors à
Il convient de noter que la VA01 d’une obligation est négative puisqu’une augmentation des taux réduit la valeur de l’obligation.
Dans le présent article, je désignerai l’un ou l’ensemble des éléments susmentionnés comme des mesures de GAP ou simplement des mesures.
Illustration des défis relatifs aux mesures ci-dessus à l’aide de CPG
J’utiliserai un exemple simple de certificat de placement garanti (CPG) pour illustrer les limites et les difficultés auxquelles sont exposées les mesures susmentionnées.
Comment les changements sont appliqués au calcul des mesures
Pour réduire le risque de taux d’intérêt, on choisit un panier d’actifs dont les mesures de la GAP correspondent à celles du passif. Pour calculer les mesures de la GAP, il conviendrait d’appliquer à l’ensemble de la courbe des taux d’intérêt une faible variation des taux (disons 10 pb), à la hausse ou à la baisse. Je traite ci-dessous de la taille de la variation et de ses répercussions. Dans le domaine des finances, bon nombre d’intervenants utilisent une variation de 25 à 50 pb. Entre autres, le recours à une variation de grande taille est justifié comme suit : puisque les mesures calculées sont ensuite utilisées pour établir des approximations de l’impact de la valeur attribuable au changement de taux, une plus grande variation atténuerait l’extrapolation implicite à l’aide des mesures appliquées aux changements de taux au-delà de la taille de la variation. Un autre motif du recours à des variations plus élevées peut découler du fait que bon nombre d’intervenants n’ont utilisé que l’appariement des durations (c.-à-d. qu’ils n’ont pas recouru à la convexité) et souhaitaient donc saisir un élément de variation de la convexité dans l’approximation de premier ordre.
Situations où les mesures de la GAP fournissent des prévisions moins fiables
La volatilité des flux de trésorerie autour des points d’inflexion limitera l’efficacité du recours aux mesures de la GAP pour prévoir les variations de la valeur du passif.
Taille de la variation
Il convient de noter que la VA01 représente la pente des lignes tangentes du graphique de la valeur des taux quand une variation proche de zéro (1 pb ou moins) est appliquée. Lorsque la variation est plus grande, elle correspond à la pente des valeurs de raccordement du cordon créées par le déplacement positif ou négatif des taux.
Pour approfondir cette observation, j’utilise un exemple simple. Supposons un contrat de CPG simple d’une valeur de 1 000 $, à taux minimal garanti de 3 %, et à marge bénéficiaire de 2 %, et permettant un retrait partiel de 10 % par année projeté sur 30 ans, après quoi le contrat est entièrement racheté. Les taux au comptant sont présumés nivelés pour cet exemple simple.
À partir de la figure 1, on peut noter un point d’inflexion à 5 % (taux de garantie minimal de 3 % + marge bénéficiaire de 2 %) après quoi les bénéfices attendus sont fixés à 2 % de la valeur du compte. Il convient de noter que la convexité de la variation de la valeur passe de négative à positive à 5 %, comme le montrent les graphiques de la figure 1. Les deuxième et troisième graphiques sont les mêmes que le premier, mais avec un zoom pour tenir compte des valeurs en utilisant des taux au comptant fixes inférieurs à 5 % et supérieurs à 5 % avec un polynôme quadratique ajusté aux graphiques pour souligner la variation de convexité.
Un point sur le graphique et ses points adjacents représentent la valeur au point et aux points utilisés dans le calcul des déplacements vers le haut et vers le bas qui produiront la VA01 et la VC01.
Notons que le signe du coefficient de x2 dans la courbe ajustée (signe de convexité) à la valeur passe de négatif à positif à 5 %, ce qui fait de 5 % un point d’inflexion. Ceci est important, car lorsque la VA01 et la VC01 servent à estimer la variation de la valeur après un déplacement, on suppose que la valeur est maintenue dans l’ensemble de la fonction quadratique ajustée aux trois valeurs calculées au taux au comptant et au taux au comptant plus et moins le déplacement. Cette importance devient évidente ci-dessous.
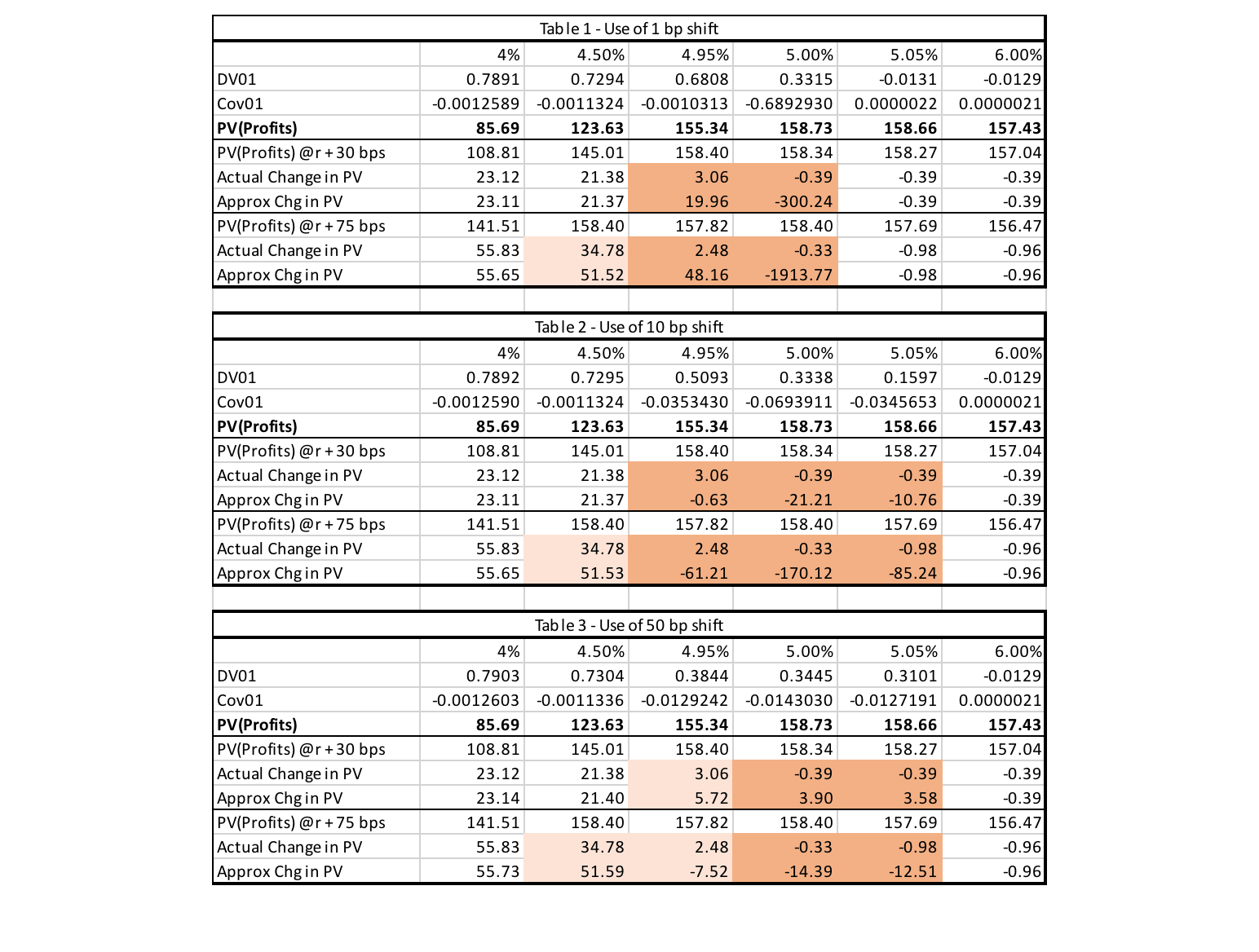
Considérons d’abord que le déplacement est minime, de sorte que le taux au comptant et le taux au comptant plus et moins le déplacement sont situés d’un côté du point d’inflexion. Puis, la meilleure approximation obtenue à l’aide de la VA01 et de la VC01 à partir de ces points ne peut être raisonnablement exacte que pour les approximations appliquées aux variations de taux qui sont inférieures ou égales à la différence entre le point d’inflexion et le taux au comptant actuel. Pour appliquer une valeur numérique à notre exemple, supposons que le taux au comptant actuel s’élève à 4,5 % et que la VA01 et la VC01 ont été calculées à l’aide d’un déplacement de 10 pb. L’approximation de la valeur d’une augmentation des taux est des plus exactes jusqu’à un maximum de 50 pb (5 % à 4,5 %). L’approximation fondée sur des variations de plus de 50 pb est moins fiable, et la valeur calculée pourrait être proche ou sensiblement différente de la valeur réelle selon le niveau de variation de la convexité après le point d’inflexion et le niveau de variation de taux supérieur à 50 pb. C’est ce que montrent les tableaux 1 à 3 ci-dessous, dans la deuxième colonne (4,5 %). Il convient de noter que peu importe le niveau de variation (1, 10 et 50 pb), l’approximation est passablement exacte pour une augmentation de taux de 30 pb (jusqu’à 4,8 %, ce qui est inférieur à 5 %, c’est-à-dire au point d’inflexion). Toutefois, l’approximation n’est plus exacte avec une variation de 75 pb, où le taux obtenu est de 5,25 % (au-delà du point d’inflexion).
Examinons maintenant la situation où le niveau de changement place les points de calcul de chaque côté du point d’inflexion. Par exemple, le taux au comptant actuel est de 4,95 % et un changement de 10 pb est appliqué. Cela signifie que la fonction quadratique à utiliser pour le calcul de la VA01 et de la VC01 (appliquée à l’approximation de la valeur de la variation des taux) est ajustée en fonction des valeurs à 4,85 %, 4,95 % et 5,05 %. Notons que deux de ces points se trouvent sous le point d’inflexion et que l’autre est au-dessus. Cela produira une fonction à convexité négative dont la valeur maximale est atteinte en deçà de 5,05 %. Toute approximation pour des taux supérieurs à 5,05 % n’est pas digne de confiance, car pour une augmentation du taux, l’approximation produira une valeur qui serait inférieure à la valeur réelle (à noter qu’au-delà de 5 %, la convexité du graphique de la valeur par rapport au comptant devient positive avec une envergure beaucoup moins grande). C’est ce que montrent les tableaux 1 à 3 ci-dessous, à la troisième colonne (4,95 %). Les variations de 30 pb et de 75 pb produisent de mauvaises approximations, peu importe la taille de la variation. Il convient de préciser que l’inexactitude des approximations obtenues en appliquant une variation de 50 pb est moins grave simplement parce qu’une plus grande partie de la valeur supérieure à 5 % est utilisée pour calculer la VA01/VC01. Toutefois, si nous avions calculé une diminution des taux (disons -30 pb ou -75 pb), l’approximation obtenue par une variation de 50 pb aurait produit de moins bons résultats puisqu’une plus grande partie des valeurs calculées étaient fondées sur des valeurs inférieures à 5 %.
Si l’on veut s’assurer que les trois points utilisés dans le calcul de la VA01 et de la VC01 demeurent du même côté du point d’inflexion, il semble préférable que la taille de la variation soit aussi petite que possible, disons 1 pb. En effet, l’examen du tableau 1 lorsque le taux au comptant est de 4 % en combinant la VA01 et VC01 peut produire une excellente approximation même si le taux est majoré de 75 pb (55,65 contre 55,83). À noter que le taux de 4,75 % demeure inférieur à 5 %. Toutefois, l’utilisation de la même variation de 1 pb lorsque le taux est 4,5 % ne produit pas une aussi bonne approximation, les taux augmentant de 75 pb pour atteindre 5,25 % (51,52 contre 34,78). La situation s’aggrave lorsque le taux actuel est de 4,95 %. Même une augmentation de 30 pb à 5,25 % produit une mauvaise approximation (19,96 contre 3,06). Cependant, une fois que les taux actuels dépassent 5,5 %, en veillant à ce que tous les taux utilisés dans le calcul de la VA01/VC01 se trouvent d’un côté du point d’inflexion, toutes les approximations redeviennent précises (voir les dernières colonnes des tableaux 1 à 3) pour les taux qui ne croisent pas le point d’inflexion (c.-à-d. une augmentation des taux ou une diminution d’au plus 50 pb).
Examinons maintenant ce qui se passe si la taille de la variation utilisée dans le calcul de la VA01 et de la VC01 est plus grande. Le tableau 2 présente les résultats d’une variation de 10 pb, tandis que le tableau 3 affiche les résultats d’une variation de 50 pb. Utilisons maintenant une variation de 50 pb (tableau 3). De toute évidence, il est plus probable que les taux utilisés dans le calcul de la VA01 et de la VC01 se trouvent des côtés opposés du point d’inflexion. Cela signifie que nous utilisons une fonction quadratique qui n’est ni proche de celle qui correspond aux valeurs avant le point d’inflexion ni près de celle qui suit. Il s’agit d’une combinaison des deux. Étant donné que cette fonction reflète un peu des deux fonctions quadratiques, elle améliore légèrement l’approximation. Par exemple, lorsque le taux actuel est de 4,95 %, l’utilisation d’une augmentation de taux de 30 pb produit une variation de la valeur de 5,72 (comparativement à 19,96 en utilisant une hausse de 1 pb) par rapport à la valeur réelle de 3,06. Et lorsque l’augmentation du taux est de 75 pb, elle produit une variation de -7,52 (comparativement à +48,16 en utilisant une hausse de 1 pb) par rapport à la valeur réelle de +2,48. Il convient de noter que même si l’erreur est réduite, l’approximation est loin d’être exacte et ne peut être utilisée pour prendre quelque décision que ce soit.
Il convient de noter que l’exemple ci-dessus était très simpliste pour souligner le problème. En ce qui concerne divers actifs et passifs, on ne produirait normalement pas de tels graphiques pour déterminer à quel point on peut se fier aux mesures et à quels changements de taux peuvent se produire les points d’inflexion. De plus, lorsqu’on apparie la duration et la convexité des actifs et des passifs, on doit se rendre compte qu’on peut s’appuyer sur ces mesures pour établir des fourchettes différentes entre les actifs et les passifs. Ainsi, la fourchette sur laquelle on peut se fonder pour déterminer l’excédent est l’intersection de la fourchette de validité des actifs et des passifs (plus petite que l’une ou l’autre des fourchettes). Je recommande en outre d’évaluer ces indicateurs directement en fonction de l’excédent, si possible, plutôt que séparément des actifs et des passifs. Dans la prochaine partie du présent article à plusieurs volets, j’énoncerai une technique pour déterminer où se produisent ces points d’inflexion et comment les mesures peuvent être ajustées pour estimer la valeur de l’instrument pour les variations de taux qui croiseraient le point d’inflexion.
Les faits énoncés et les opinions formulées dans le présent document sont ceux de chaque auteur et ne correspondent pas nécessairement à ceux de la Society of Actuaries, des rédacteurs du bulletin ou des employeurs des auteurs.
Dariush Akhtari, FSA, FICA, MAAA, est actuaire en chef chez Converge RE. On peut le joindre à dakhtari@converge-re.com.