Intégration de la science des systèmes dans la gestion du risque : Partie 1 — Démystifier le risque, l’équilibre et les chocs exogènes
par Bryon Robidoux
Gestion du risque, février 2024

Le présent article est le premier d’une série portant sur l’amélioration de la gestion du risque au sein d’une société d’assurances sous l’angle des théories de la complexité, du calcul et de l’information. Ces théories nous obligeront à repenser les concepts statiques du risque, de l’équilibre et des chocs et à les remplacer par des principes dynamiques d’incertitude, d’émergence et de rétroaction. Pour ce faire, il faut comprendre leurs inconvénients et les limites extrêmes du risque, de l’équilibre et des chocs, car ils constituent le fondement de nos processus de gestion du risque.
Pourquoi le risque est-il une possibilité?
Vous êtes-vous déjà demandé d’où provient le dicton : « Le risque, c’est la possibilité? » Pourquoi ne dit-on pas que « l’incertitude est une possibilité »? La raison est fondamentale pour bien comprendre les limites des mesures de risque.
Selon la théorie des marchés financiers, [traduction] « le risque représente une situation où un agent ou une agente ne peut observer l’état immédiat du monde, mais a une connaissance complète de l’espace de probabilité. L’incertitude a trait à une situation où un agent ou une agente ne connaît pas parfaitement la probabilité des événements. »[1] Comme le fait valoir l’ouvrage « Real Options in Radical Uncertainty: Part 1—The Nature of Risk and Uncertainty » (ROP1), on ne peut connaître les résultats avec certitude qu’au casino parce que les gestionnaires de casino définissent les règles de jeu. Par exemple, nous connaissons tous le nombre de jeux de cartes que renferme le sabot au blackjack; il est donc possible de connaître la probabilité d’un résultat particulier. Le risque est une possibilité parce que le joueur ou la joueuse peut apprendre les chances d’obtenir un résultat précis avant de jouer sa main.
Dans le monde physique à l’extérieur des casinos, personne ne peut connaître tous les résultats avec certitude. Le risque représente une ludification des événements, tandis que l’incertitude est un calcul des événements fondé sur l’innovation universelle du monde physique. Les résultats possibles changent à chaque fois que l’univers calcule son état suivant, de sorte qu’il est impossible de connaître tous les résultats possibles. Même si l’on utilise les termes risque et incertitude comme synonymes, ce sont des concepts très différents aux origines très différentes. En tant qu’actuaires, nous n’émettons jamais de polices dans un casino, de sorte que nous ne gérons jamais le risque. Par ailleurs, les actuaires sont constamment confrontés à des événements incertains, comme des catastrophes et des garanties du marché.
Limites du risque
L’article intitulé « Real Options in Radical Uncertainty: Part 2—The Limits of Financial Option Theory » (ROP2) explique que les préférences en matière de risque, comme la neutralité du risque, ne sont pas définies dans le monde physique au moyen de la théorie des perspectives. La définition d’un investisseur risque-neutre est un agent ou une agente indifférent(e) entre un résultat garanti à l’échéance et un pari risqué avec un résultat attendu à l’échéance égal au résultat garanti à l’échéance. Un agent ou une agente ne consentirait à ce compromis que s’il ou elle connaissait avec certitude l’espace de probabilité sous‑jacent. Dans un monde incertain, rien ne garantit que les agent(e)s puissent calculer de façon fiable la valeur attendue, de sorte qu’il existe une différence entre la teneur en information d’un résultat à l’échéance certain et celle d’un résultat à l’échéance attendu. Cette différence d’information explique l’indifférence présumée entre les résultats certains et attendus et les résultats empiriques de la théorie des perspectives. Les éléments de preuve empiriques montrent que le risque et l’incertitude engendreront des décisions différentes, de sorte qu’il est erroné d’utiliser des constatations fondées sur des mesures du risque pour gérer l’incertitude.
Information
Dans ROP2, j’ai commis une erreur dans l’analyse risque-neutre, ce qu’un de mes collègues a souligné. L’erreur ne modifie pas la conclusion sur les préférences en matière d’information par rapport aux préférences au chapitre du risque, mais elle constitue une excellente occasion d’apprentissage. J’ai déclaré qu’un résultat certain contient plus d’information qu’une attente incertaine, mais c’est le contraire. Selon Wikipédia, [traduction]« l’information de Shannon est interprétée comme quantifiant le niveau de « surprise » d’un résultat particulier. » Les gens préfèrent des paiements certains plutôt que la valeur attendue incertaine parce qu’un résultat certain ne réserve aucune surprise. Par conséquent, les paiements certains ne contiennent aucune information. Par contre, une attente incertaine peut avoir un résultat imprévisible parce qu’elle contient des renseignements non pris en compte.
Changement fondamental apporté aux processus de gestion du risque
Par conséquent, cette correction permet de conclure qu’il manque une étape dans tous les processus de gestion du risque. Le risque suppose l’impossible : N’importe qui peut connaître avec certitude tous les résultats possibles du monde physique. Par définition, le risque balaie une grande partie de l’incertitude et des résultats possibles sous le tapis. Si le risque était un tapis, il aurait la taille d’un paillasson. Mais la taille de l’incertitude sous le tapis occupe l’espace d’un immeuble de 20 étages! Le risque nous rend beaucoup trop confiants.
Steven Keen décrit trois types d’hypothèses: négligeable, domaine et heuristique.
- Les hypothèses négligeables ont peu ou pas d'impact sur le phénomène étudié.
- Les hypothèses de domaine précisent les principales conditions dans lesquelles une théorie s'appliquera.
- Les suppositions heuristiques sont des suppositions connues comme étant fausses, qui sont les premières étapes d'une théorie générale. Ces hypothèses sont énoncées et utilisées pour simplifier dans un premier temps, puis assouplies dans un second temps pour terminer correctement la thèse.[2]
Les ouvrages contemporains sur la gestion du risque traitent du risque à titre d’hypothèse de domaine, ce qui repousse l’incertitude. Toutefois, le risque devrait être une hypothèse heuristique. La certitude de l’espace de probabilité sous-jacent doit être assoupli. L’écart dans les résultats de mesure avant et après l’assouplissement de la certitude est connu comme le risque. Autrement dit, le risque représente le degré de certitude auquel le ou la gestionnaire de risques dispose de l’espace de probabilité sous-jacent et de la distribution présumée. La certitude totale est une mesure risquée. Aucune certitude n’est une mesure tout à fait incertaine, comme une courbe de rendement projetée dans 50 ans. Le degré de risque détermine comment l’intervalle de confiance peut être étroit pour la mesure.
L’absence d’incertitude ne sous-entend pas son inexistence; il est donc essentiel de mesurer le niveau de confiance. Quel est le bienfait des activités de gestion des risques, comme l’optimisation du portefeuille, l’immunisation ou l’atténuation du risque, sans mesurer ou du moins exprimer l’incertitude liée à leurs résultats? Dans quelle mesure est-il logique d’optimiser votre portefeuille pour ensuite réaliser qu’il contient de nombreuses incertitudes et que des informations sont manquantes, ce qui invalide la réponse? En quoi cela contribue-t-il à accroître la fiabilité de nos activités d’assurance?
Limites de l’équilibre
À l’instar du risque, l’équilibre représente une vision statique ludique du monde. Lorsque la roue de la roulette tourne dans un casino, elle finit par s’arrêter quand elle atteint son point d’équilibre. Chaque partie du jeu est indépendante de la précédente ou de la suivante. À l’équilibre, le croupier ou la croupière détermine les résultats; et la partie recommence.
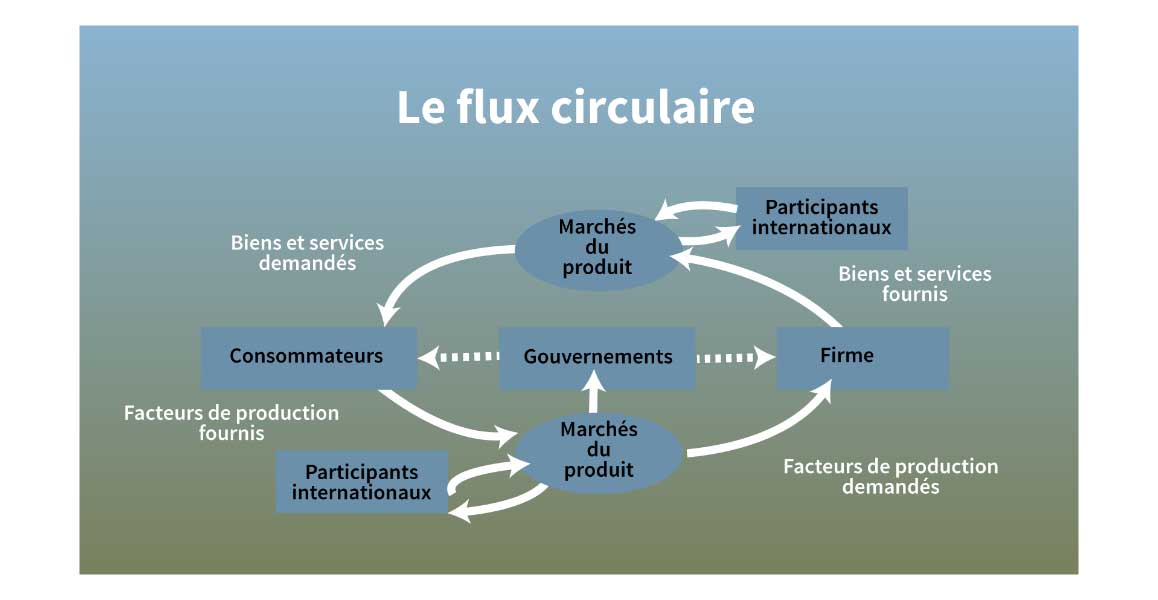
Figure 1
Introduction aux flux et à l’énergie
Cette photo d’un auteur inconnu fait l’objet d’un permis aux termes de CC BY-SA-NC
Dans Doughnut Economics: 7 Ways to Think Like a 21st Century Economist, Kate Raworth décrit comment, en 1948, Paul Samuelson a créé une machine appelée Monetary National Income Analogue Computer (MONIAC) pour montrer le flux circulaire des revenus dans l’économie du Royaume-Uni. Il a utilisé des réservoirs et des tuyaux pour démontrer la théorie de John Maynard Keynes sur la façon dont les économies pouvaient se retrouver dans la spirale de la récession. Il s’agissait d’une brillante représentation visuelle des idées macroéconomiques encore utilisées aujourd’hui.
Raworth souligne que l’appareil de Samuelson devait être branché dans une prise électrique pour alimenter toutes les pompes afin que l’eau puisse circuler à travers le modèle. Pourtant, nulle part dans son explication sur la macroéconomie Samuelson n’a-t-il expliqué la contribution de l’énergie dans le flux de revenus[3]. La seule façon qui aurait permis à MONIAC d’atteindre l’équilibre consistait à la débrancher du mur, ce qui aurait tué à la fois la machine et l’économie! Comme c’est souvent le cas, les modèles macroéconomiques considèrent l’énergie comme un intrant économique secondaire. L’énergie et le calcul devraient être considérés comme l’élément principal de l’économie[4].
La mort de l’équilibre
Dans le monde physique, l’incertitude est l’antithèse de l’équilibre. Selon ROP1, l’incertitude découle du calcul, créant un résultat ordonné à partir d’intrants désordonnés à l’aide de l’énergie. Par exemple, si un système contient deux atomes d’hydrogène et que l’on y applique suffisamment d’énergie, ils fusionneront pour former un atome d’hélium. Par conséquent, l’influx d’énergie a fait en sorte que le processus est passé d’un état moins ordonné à un état plus ordonné où les réactions chimiques agissent comme des transistors primitifs.[5] La nouvelle forme de la matière se solidifie en information. Seuls les systèmes qui se situent loin de l’équilibre et qui sont remplis d’énergie sont soumis à ce processus de calcul. L’utilisation d’une plus grande quantité d’énergie produit davantage de calculs, créant ainsi plus d’information et de structures complexes, qui constituent la base de l’innovation universelle.
Seuls les systèmes éloignés de l’équilibre et débordant d’énergie localisée peuvent créer un ordre physique dans les poches de l’univers, comme la Terre. Lorsque l’énergie est retirée, l’entropie transforme l’ordre en désordre, l’objet se désintègre et l’ordre physique est perdu. Les systèmes en équilibre et en complet désordre sont morts[5]. L’innovation universelle a créé toute la vie qui ne pouvait exister sans information, calcul et énergie. Sans la vie humaine et l’énergie du soleil, l’économie ne pourrait pas exister. Keen appelle cela le mauvais équilibre[4] parce que l’économie est morte!
Un équilibre en dehors de la mort peut exister, ce que Keen appelle un bon équilibre pour des raisons évidentes. Keen explique que l’économie ne se stabilise pas en équilibre et qu’elle est ensuite exposée à un choc qui lui faire perdre l’équilibre, et qu’elle recommence toujours sa progression vers l’équilibre. L’économie dispose d’une dynamique non linéaire, ce qui signifie qu’elle se comporte différemment lorsqu’elle est éloignée de l’équilibre ou qu’elle en est proche. Il est probable que lorsque l’économie est éloignée de l’équilibre, elle s’en rapproche, mais à un moment donné, avant d’atteindre l’équilibre, les forces changent et l’en éloignent. Ce processus créera un cycle sans fin au sein de l’économie, ce qui va à l’encontre de ce qu’on nous a enseigné en économie. L’équilibre n’est pas garanti ou ne devrait pas être perçu comme devant se produire. Le seul équilibre garanti est la mort!
Limites des chocs exogènes
L’univers est un système qui renferme notre système solaire. Notre système solaire comprend la Terre. La Terre est une organisation de la géologie et un écosystème vivant. Dans l’écosystème, les humains ont un processus de commerce appelé économie. À mesure que l’énergie circule, l’innovation universelle crée de façon récursive de nouveaux états. Il n’existe pas d’idée comme étant exogène d’un système ou de l’économie. Par conséquent, aucun choc exogène ne fait bouger l’économie d’un état à l’autre.
Autres problèmes liés aux chocs
Dans les exercices de gestion des risques, nous soumettons souvent les variables du modèle à des chocs pour déterminer l’incidence d’un changement afin de calculer les expositions à un risque. J’aimerais aborder trois problèmes :
- la criticité et les points d’inflexion;
- les distributions à faible valeur extrême;
- les attentes.
Criticité et points d’inflexion
Il est essentiel de connaître et de comprendre la dynamique sous-jacente des systèmes que nous modélisons. Les systèmes stables peuvent avoir un point d’inflexion où ils modifient le comportement. Le point d’inflexion peut même être un point critique où le système tombe en panne. Parmi les exemples de points d’inflexion, mentionnons la déchéance du choc à la fin de la période d’imposition des frais de rachat d’une rente variable ou le passage de l’eau en glace. Un exemple de point critique est une pente de ski juste avant une avalanche. Si les modèles n’intègrent pas ces mécanismes, ils se comporteront de façon incorrecte.
Distributions à faible valeur extrême
ROP2 indique que : [traduction] « La distribution gaussienne est surtout associée au théorème central limite. Ce théorème devrait être renommé théorème de la limite centrale parce qu’il traite du centre de la distribution. Le théorème central limite indique que, pour les échantillons indépendants et identiquement distribués, la moyenne de l’échantillon fusionne avec la distribution normale ou gaussienne même si les échantillons originaux ne font pas l’objet d’une distribution normale. La probabilité d’écart par rapport à la moyenne ou au centre de la distribution diminue de façon exponentielle avec l’ampleur de l’écart. » Notre forte dépendance à la distribution gaussienne fait en sorte que nos modèles reviennent à la moyenne, quel que soit l’ampleur du changement économique.
Valeur attendue
Envisageons cela comme la loi de Hooke en physique. Selon Wikipédia, [traduction] « Il s’agit de la force (F) nécessaire pour allonger ou comprimer un ressort d’une certaine distance (x) qui s’adapte linéairement en fonction de cette distance, c’est‑à‑dire F = kx, où k est un facteur constant caractéristique du ressort (c.-à-d. sa rigidité), et x est faible par rapport à la déformation totale possible du ressort. » Les ressorts sont calibrés pour connaître leur résistance et la quantité maximale à laquelle s’applique la loi de Hooke. Mais à un moment donné, le ressort atteindra son point de rupture, le point d’inflexion où la loi de Hooke est inapplicable ou inopérante. Imaginez que le ressort peut supporter jusqu’à cinq kilogrammes, mais vous ajoutez sept kilogrammes. Le ressort se déformera légèrement. Il continuera probablement de fonctionner, mais pas selon la loi de Hooke. Ajoutez maintenant 500 kilogrammes, ce qui ruinera le ressort.
Lorsque nous effectuons une simulation de Monte-Carlo avec des scénarios de fortes fluctuations du marché ou d’importants chocs pour déterminer les variables Grecques, nous supposons qu’il n’y a pas de limite apparente d’élasticité. Ainsi, le marché reviendra à son état d’origine et se comportera comme il l’a toujours fait par magie. Mais nous savons que ce n’est pas vrai; les marchés ont des points d’inflexion et des points critiques lorsqu’ils se comportent différemment et se déforment. John Kay et Mervyn King affirment qu’il est peu utile d’introduire des chocs ou de simuler d’importants déplacements du marché sans modéliser l’inflexion sous-jacente et les points critiques. Il est peu utile d’ajouter des sauts aléatoires sans comprendre la dynamique sous-jacente[6]. Comme nos modèles économiques se concentrent sur la valeur attendue, ils sont probablement incorrects aux extrémités. Le modèle soumis à un choc axé sur les attentes donnera des résultats très différents par rapport à la valeur attendue d’un modèle intégrant des points d’inflexion et des points critiques.
Conclusion
La gestion du risque est une activité essentielle en assurance. En examinant de près la définition du risque, il devient immédiatement évident que des améliorations doivent y être apportées. Le livre intitulé Modern Investment Management: An Equilibrium Approach mentionne que [traduction] « si l’on suppose que les marchés sont irrationnels, il y a peu à ajouter. Peut-être pourrions-nous trouver quelques modèles d’irrationalité, mais pourquoi devraient-ils persister? » [7] Cette opinion prend son origine dans le risque, l’équilibre et les chocs exogènes. Je crois que cette attitude est typique et qu’elle nous freine.
Nous savons que les humains sont irrationnels, et la vie ne fonctionne pas comme les jeux. J’ai démontré que les décisions fondées sur le risque mèneront à des conclusions différentes de celles émanant de l’incertitude, ce qui signifie que l’on gagne peu en s’accrochant au risque. Nous ne pouvons pas apprendre à composer avec l’incertitude si nous refusons d’y faire face. Nous devons élaborer de nouvelles solutions et de nouveaux outils pour composer avec l’incertitude.
Pour comprendre l’importance de la science des systèmes et sa puissance dans la gestion du risque, il est essentiel de comprendre les faiblesses des approches actuelles. Le présent article a montré que :
- Les indicateurs de risque supposent une certitude et des renseignements que personne ne peut posséder.
- L’économie donne l’impression que les processus se dirigent toujours vers l’équilibre, mais vers la linéarité supposée dans les modèles économiques.
- Les chocs exogènes sur l’économie ne sont pas possibles parce que l’économie est un système qui se déplace d’un état à l’autre au moyen de calculs et de l’innovation universelle.
Les vues du monde simplifiées à outrance conduisent à des solutions radicalement trop simples et incorrectes. En supposant une connaissance complète de tous les résultats, nous sommes beaucoup plus confiants que nécessaire dans les résultats de nos modèles. Pour améliorer nos capacités de gestion, nous devons gérer l’incertitude à laquelle nous sommes confrontés.
Les faits énoncés et les opinions formulées dans le présent document sont ceux de chaque auteur et ne correspondent pas nécessairement à ceux de la Society of Actuaries, des rédacteurs du bulletin ou des employeurs des auteurs.
Bryon Robidoux, FSA, CERA, est vice-président adjoint du développement des produits auprès de Constellation Insurance. Vous pouvez le joindre à bryon_robidoux@ConstellationInsurance.com.