Intégration de la science des systèmes dans la gestion du risque : Partie 2 – Comprendre la complexité, l’émergence et l’interdépendance
par Bryon Robidoux
Gestion du risque, juin 2024

La partie 1 de l’article visait à repenser les concepts de risque, d’équilibre, de chocs, et leurs limites, des concepts importants en actuariat et en économie. Le présent article présente une façon différente d’aborder l’économie du point de vue de la science des systèmes et introduit des concepts comme la complexité, l’émergence et l’interdépendance. Les concepts permettent une meilleure conformité au comportement des marchés et des titulaires de polices. J’expliquerai d’abord ce que l’on entend par science des systèmes, puis je définirai la complexité désorganisée et la complexité organisée et je décrirai la puissance d’inclure l’interdépendance dans les modèles financiers.
Pourquoi la science des systèmes?
Alors que le monde devient de plus en plus complexe et incertain, il y a une tendance à se spécialiser et à creuser profondément dans les problèmes. L’humanité est au point de son évolution où les problèmes sont rarement résolus en creusant plus profondément dans des cloisons spécialisées. Alors que nous réfléchissons à la résolution des problèmes à venir, nous devons créer une vue d’ensemble. Nous devons trouver des facteurs communs entre les questions portant sur de nombreuses disciplines parce que l’actuariat n’est pas une discipline autonome, mais un rassemblement d’éléments d’affaires, de finances, de mathématiques, d’informatique, de psychologie et d’écologie. Pensez simplement à tous les différents sujets qu’abordent les actuaires. Il est difficile de nous définir et de nous confiner dans une boîte.
Selon les Principles of System Science, [traduction] « la science des systèmes s’emploie à comprendre les systèmes. Elle examine les attributs, la dynamique, les caractéristiques et les comportements utiles des systèmes en tant que systèmes, y compris les principales différences entre les sous-catégories de systèmes, entre autres linéaires, non linéaires, fermés, ouverts et complexes. » La science des systèmes ne se soucie pas du fait que les systèmes sont écologiques, sociaux, physiques ou chimiques; elle s’attarde aux points communs qui les unissent.[1] À mesure que les actuaires aborderont des domaines comme les changements climatiques, il sera utile d’établir des liens entre les systèmes économiques et écologiques.
Le problème
Mais à mon avis, il existe un problème : l’économie, la gestion des risques et l’actuariat, qui sont au cœur de notre profession, simplifient grandement le fonctionnement de l’économie, et ce, à leur détriment. L’économie aime construire ses théories à partir de principes premiers axiomatiques.[2] La traçabilité des mathématiques repose d’abord sur l’hypothèse voulant qu’elle rende l’économie linéaire. Dans des systèmes linéaires, la somme est égale à l’ensemble des parties, de sorte que vous pouvez les comprendre en les disséquant dans leurs éléments indépendants. Le comportement qui en découle provient de l’agrégation des éléments indépendants.[3] De plus, la linéarité permet de prédire facilement le comportement futur, ce qui explique la préférence qui lui est accordée en économie. L’économie devient une machine prévisible comme les corps célestes qui flottent autour de notre système solaire; cette machine ne nécessite aucune coordination ou organisation pour fonctionner de façon correcte.
L’émergence désorganisée
L’économie nous réserve toujours des événements aléatoires. L’émergence d’un comportement à partir de la somme d’événements aléatoires indépendants est appelée « processus additif », de sorte que ![]() où chaque élément Xi est une variable aléatoire indépendante et identiquement distribuée. Les processus additifs représentent l’origine de la loi des grands nombres et du théorème de la limite centrale, qui sont des approximations de premier et de deuxième ordres des processus additifs, respectivement. De façon informelle, la loi des grands nombres indique que Sn est bien approximée par sa moyenne µ, qui est la valeur attendue de Xi. De plus, tout le caractère aléatoire de Sn a disparu et n’est qu’une fonction de n et de sa moyenne µ, i.e.
où chaque élément Xi est une variable aléatoire indépendante et identiquement distribuée. Les processus additifs représentent l’origine de la loi des grands nombres et du théorème de la limite centrale, qui sont des approximations de premier et de deuxième ordres des processus additifs, respectivement. De façon informelle, la loi des grands nombres indique que Sn est bien approximée par sa moyenne µ, qui est la valeur attendue de Xi. De plus, tout le caractère aléatoire de Sn a disparu et n’est qu’une fonction de n et de sa moyenne µ, i.e. ![]() [4]
[4]
Le théorème de la limite centrale est un terme de correction de second ordre qui saisit le caractère aléatoire des processus additifs. Étant donné que la variance de Xi est finie, elle indique que ![]() , où
, où ![]() . Sn − nµ est l’erreur et s’approche de la distribution gaussienne de l’ordre de
. Sn − nµ est l’erreur et s’approche de la distribution gaussienne de l’ordre de ![]() La combinaison de la loi des grands nombres et du théorème de la limite centrale indique que le processus additif, Sn, , peut être calculé par approximation au moyen de
La combinaison de la loi des grands nombres et du théorème de la limite centrale indique que le processus additif, Sn, , peut être calculé par approximation au moyen de ![]() [5]
[5]
Les processus additifs comportent des caractéristiques pratiques. Il n’est pas nécessaire que les variables aléatoires soient des variables gaussiennes distribuées pour que cela se produise. Les variables aléatoires Xi peuvent être réparties de nombreuses façons. Comme seule exigence, elles doivent être indépendantes et identiquement distribuées, ce qui est incroyable. Cette exigence est appelée complexité désorganisée parce qu’il n’existe pas de coordination ou de dépendance entre les événements [6]
De plus, à mesure que n augmente, les processus additifs se dirigent de façon exponentielle vers la moyenne, ce qui signifie que les valeurs aberrantes importantes sont rares. S’il y a suffisamment d’événements importants, les bons résultats neutralisent les mauvais résultats importants, et ils s’annulent mutuellement. Ce scénario crée une rétroaction négative parce qu’il fera en sorte qu’un système atteindra un équilibre stable à peu près à sa moyenne. [7] Ces processus additifs constituent le fondement de nos modèles de gestion des risques et de couverture, ce qui est regrettable parce que la crise financière de 2008 ne se serait jamais produite si l’économie s’était approchée d’un processus additif. Dans son livre, The Black Swan, Nassim Nicholas Taleb met en garde contre les modèles économiques qui reposent sur des processus additifs pour modéliser la dynamique du marché et il préconise le recours aux théories de Mandelbrot.[8]
La solution
L’économie n’est composée d’aucun événement indépendant. Ne cherchez pas plus loin que la COVID-19 pour voir comment le monde est massivement interconnecté. Cette interconnectivité signifie que les événements dépendent les uns des autres. Ces événements interdépendants mènent à des processus multiplicatifs non linéaires comme les fractales et les lois de puissances. Dans son livre intitulé The (Mis)Behavior of Markets, Mandelbrot soutient que la théorie du marché devrait adopter des fractales et des lois de puissance de complexité organisée [9].
L’émergence organisée
Selon Paul Fieguth, « le méta-comportement du système, induit par le couplage non linéaire de nombreux éléments, est un phénomène émergent. Un comportement émergent porte sur l’idée classique du « tout supérieur à la somme des parties »[10] Il est presque impossible de modéliser le comportement émergent au moyen d’une analyse en raison des nombreuses réactions. La simulation est possible, mais sa puissance prédictive peut poser problème parce que les résultats dépendent fortement de l’état initial.[11]
Un système complexe présente des comportements émergents et auto-organisés non anodins.[12] Dans le cas de la complexité organisée, les interactions sont interdépendantes et se renforcent mutuellement par rétroaction positive. Il existe une complexité organisée dans les systèmes qui évoluent, s’adaptent et s’organisent eux-mêmes. La complexité organisée se produit en cas d’effondrement des marchés boursiers, d’émeute, d’embouteillage, de panique bancaire, de tremblement de terre, d’inondation et d’incendie[13]—les risques incertains que l’assurance promet de couvrir.
On comprend la complexité organisée en regroupant les éléments interdépendants pour savoir comment fonctionne le système dans son ensemble. C’est pourquoi la chimie n’est pas seulement de la physique appliquée, la biologie n’est pas de la chimie appliquée et l’écologie n’est pas de la biologie appliquée[14]
Émergence de l’efficacité et de la stabilité
Comme je l’ai mentionné dans Adam Smith and Evolutionary Economics, la théorie économique dominante suppose que la robustesse et la stabilité des marchés sont aussi fiables que la gravité et qu’elles existent en raison d’une complexité désorganisée.[15] Dans la partie 1 du présent article, j’ai expliqué qu’il existe deux types d’équilibre : le mauvais et le bon. Le mauvais équilibre, la mort, est le seul équilibre garanti. Un bon équilibre, c’est l’homéostasie, mais ce n’est jamais garanti. Des systèmes non linéaires et interconnectés émergent avec des comportements différents proches plutôt qu’éloignés de l’équilibre.[16]
Les systèmes adaptatifs articulés et complexes (SAC) d’Adam Smith ont montré que l’équilibre est une propriété émergente de la coopération et de la collaboration des compétences hétérogènes à de nombreux niveaux effectuant une recherche en parallèle, ce qui permet d’atteindre la stabilité et l’efficacité du marché, ce qu’Adam Smith a perçu comme la main invisible. (Cette interprétation est très différente de l’interprétation de la main invisible en vertu de l’économie traditionnelle.) Au cours de la recherche en parallèle, les intervenants interconnectés du marché fournissent des signaux fondés sur le milieu actuel pour réévaluer ce qui doit essentiellement être exploré. En termes simples, l’algorithme que les acteurs du marché utilisent à la recherche de profits n’est pas différent de l’algorithme qu’utilisent les colonies de fourmis pour chercher des aliments.[17]
L’interdépendance
Dans The New Evolutionary Microeconomics: Complexity, Competence and Adaptive Behaviour, Jason Potts distingue l’économie traditionnelle de l’économie évolutive en ce qui concerne la façon dont les deux différencient les relations entre les intervenants du marché.[18] L’économie traditionnelle suppose que les gens vivent dans un champ ou un espace intégral, ce qui signifie que toutes les relations sont 100 % fongibles et homogènes, de sorte qu’il n’y a aucune raison de modéliser les réseaux. L’accent est placé sur l’indépendance et les poursuites individualistes. L’économie évolutive suppose un espace non intégral, de sorte que les interactions et les relations en réseau varient et revêtent une importance primordiale. Parce qu’elle repose sur la théorie de la complexité, elle met l’accent sur l’interdépendance entre les intervenants du marché et la façon dont ils collaborent. Tout comme pour l’écologie, la perception est que tout est interrelié et que l’hétérogénéité est essentielle au bon fonctionnement des systèmes.[19,20]
Contagions comportementales par des intervenants interconnectés du marché
Dans Change: How to Make Big Things Happen, Damon Centola explique les contagions simples et complexes dans des contextes réseautés.[21] Les contagions simples sont des virus et des rumeurs parce qu’un simple contact avec d’autres personnes suffit pour une propagation rapide grâce à des connexions faibles. Un réseau faiblement connecté ressemble à un feu d’artifice. Les contagions complexes sont des mouvements politiques et sociaux auxquels les gens résistent et qui se propagent grâce à des liens forts. Un réseau fortement connecté ressemble à un filet de pêche avec de nombreux liens couplés de façon redondante.
Le point auquel l’infection complexe se propage est appelé le point de bascule. Lorsqu’une infection ou idée nouvelle s’immisce dans un réseau fortement connecté, la redondance entre les liens crée une immunité aux nouvelles idées et une contagion en raison des commentaires négatifs découlant des idées existantes.[22] Cette immunité est une autre source de stabilité du marché. Ce n’est qu’une fois que le réseau devient saturé au-delà de 25 % qu’il bascule, et l’infection se propage énergiquement avec une rétroaction positive, ce qui favorise de nouveaux comportements émergents. Le changement qui en résulte est beaucoup plus durable et rapide que dans un réseau faiblement connecté,[23] qui est à l’origine de dislocations et de ruptures du marché. La rétroaction positive peut facilement avoir des résultats défavorables.
Dans le présent document, je présume que le recours à la gestion des risques à l’égard des processus additifs est une simplification exagérée et irréaliste. Si c’est exact, alors pourquoi semble-t-il que les marchés sont stables la plupart du temps, comme les processus additifs semblent le prédire? Les ruptures du marché apparaissent comme des événements ponctuels, uniques et peu fréquents associés à des processus additifs.
Mais ces ruptures ne sont pas des événements uniques et ponctuels; elles sont tout à fait normales! Comprendre la stabilité des marchés, c’est comprendre comment l’information infecte les marchés et devient contagieuse. Les intervenants du marché sont fortement connectés avec de nombreuses redondances, ce qui confère à l’information une immunité de prix et une apparence de stabilité. Plus le marché sera robuste et liquide, plus il sera stable et à l’abri de la propagande infectieuse. Le marché devient instable lorsqu’il est infecté par de nouvelles informations, ce qui l’amène à atteindre son point de bascule; tandis que la rétroaction positive pousse soudainement le marché dans une nouvelle direction, loin de sa valeur prévue.
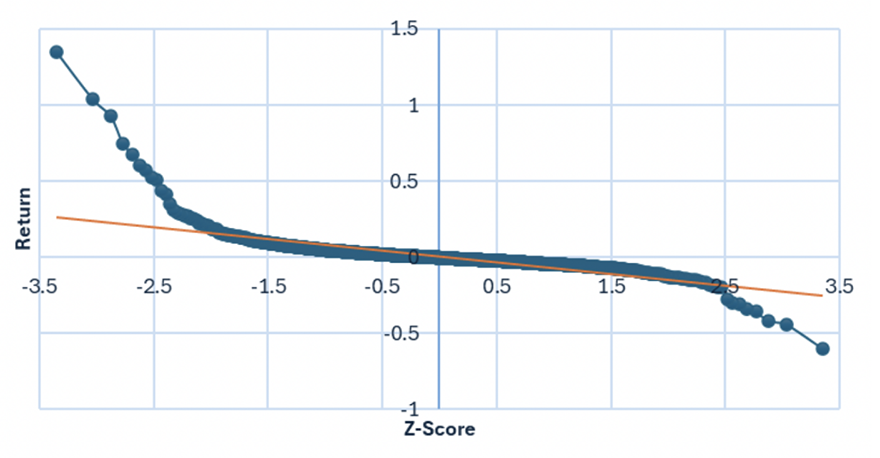
Les actions mèmes, comme GameStop et AMC Theaters, affichent des fluctuations de prix farfelues qui s’expliquent facilement par ces dynamiques de réseau, mais qui déconcertent l’optique des processus additifs. Le graphique ci-dessous montre la courbe Q-Q (quantile-quantile) de GameStop. Si les rendements provenaient d’une distribution gaussienne, les rendements en bleu devraient correspondre à la ligne de tendance orange. Comme vous pouvez le voir, c’est loin d’être le cas.
Mesure de l’interconnectivité
Dans l’économie traditionnelle, l’influence d’une variable sur une autre serait généralement mesurée au moyen de la covariance, qui est une fonction de corrélation et de volatilité.[24] La corrélation n’est pas une mesure de la force de connexion. Elle est 1(-1) lorsqu’il existe une relation linéaire positive (négative) complète. Elle est zéro en l’absence de relation. La corrélation est une mesure de linéarité [-1,1] et elle est « notoirement instable »[25] Mais pourquoi?
Comme l’explique la science cognitive, nous ne pensons pas seuls ou ne créons pas d’attentes de façon isolée. Nous nous en remettons constamment à nos pairs pour obtenir une confirmation et de la connaissance afin d’interpréter la signification des événements et créer des attentes qui exigent qu’il s’agisse d’interactions non linéaires.[26] À mesure que les opinions changent, particulièrement autour du point de bascule, le comportement des intervenants interconnectés du marché changera,[27] ce qui explique l’instabilité de la corrélation.
Avant le point de bascule du réseau, la corrélation serait stable parce que les intervenants hétérogènes du marché créent une rétroaction négative. À mesure que le réseau approche du point de bascule, les corrélations deviennent extrêmement erratiques parce que le groupe est confus sur le plan directionnel. À mesure que le groupe synchronise son comportement après avoir franchi le point de bascule, il s’établira une forte relation entre les variables, donnant un signal fort de linéarité, ce qui implique que la corrélation devrait être proche de 1 ou -1. Cette anecdote explique pourquoi les corrélations montent en flèche en cas d’effondrement du marché.
L’économie traditionnelle suppose généralement un espace intégral et une fongibilité de 100 %,[28] ce qui signifie que toutes les contagions sont simples et se propageraient de façon immédiate. Si tel était le cas, les marchés n’auraient ni stabilité ni robustesse et se déchireraient immédiatement avec des prix fulgurants. En ne supposant que des commentaires négatifs – ce qui mène par magie à l’équilibre – l’économie traditionnelle peut ignorer cette contradiction. Un bon exemple de cela serait les marchés illiquides parce que les intervenants du marché sont faiblement connectés et ne sont pas suffisamment nombreux pour que la stabilité émerge, de sorte que les prix affichent une variation considérable. Par conséquent, l’incorporation de la rétroaction positive et de l’émergence organisée dans les modèles économiques actuels est insuffisante pour intégrer la science des systèmes à la gestion des risques.
Conclusion
En fin de compte, le monde devient de plus en plus interconnecté à mesure qu’Internet prend de l’expansion. La pandémie de COVID-19 a rendu cette tendance particulièrement évidente. L’économie et la gestion des risques que nous assumons dans notre travail quotidien sont ancrées dans des principes élaborés bien avant l’ère informatique moderne des années 1950 et 1960, après la Seconde Guerre mondiale. Leon Walras a envisagé l’économie à l’équilibre général en 1874 mais c’est Debreu qui a dérivé la version de l’équilibre au cœur de notre économie aujourd’hui.[29] Le recours à des systèmes linéaires pour décrire l’économie à cette époque était logique, car les calculs ne nécessitaient pas d’ordinateurs. Même si Black et Scholes ont rendu célèbre la théorie du prix des options en 1973, Louis Bachelier (1900) a d’abord élaboré la théorie des mouvements browniens pour les marchés – une composante importante de la théorie du prix des options – dans sa thèse de doctorat. Il me semble que la théorie de la gestion des risques est équivalente à celle d’un Model T de Ford. Nous devons continuellement utiliser des pièces d’après-vente, comme les processus de sauts, pour que le système continue de fonctionner en pétaradant.
La popularité grandissante des ordinateurs dans les années 1950 a donné lieu à la naissance de la science de la complexité, un sous-ensemble de la science des systèmes qui existe aujourd’hui. Comme j’ai tenté de le démontrer, la science des systèmes nous permet d’étudier toutes sortes de systèmes, notamment des systèmes sociaux, économiques et écologiques. Elle modélise mieux la complexité et les différents types de mécanismes de rétroaction qui peuvent exister sur le marché. Les systèmes complexes peuvent être plus difficiles à utiliser pour effectuer des prédictions et ils nécessitent des ordinateurs modernes. Toutefois, je crois que les prédictions du marché fondées sur des systèmes additifs nous donnent une fausse sécurité et nous rendent trop optimistes parce qu’elles supposent une stabilité beaucoup trop grande pour le marché parce qu’elles ne tiennent compte que des commentaires négatifs. Les marchés ne bougent pas en raison d’événements indépendants, désorganisés et singuliers. Ils se déplacent en raison d’événements organisés, interdépendants et massivement parallèles. Les modèles doivent refléter la bonne dynamique, sinon ils entraîneront des décisions erronées.
En tant que gestionnaires, nous devons respecter les promesses faites aux titulaires de contrats. Nous devons nous assurer de tenir dûment compte de l’instabilité des marchés, surtout lorsqu’il y a des commentaires très positifs, notamment à l’issue de la crise financière de 2008. À mon avis, cela n’est possible que si nous comprenons mieux la science des systèmes, surtout à mesure que notre profession évolue dans de nouveaux domaines, comme l’aide à la gestion des changements climatiques.
Les faits énoncés et les opinions formulées dans le présent document sont ceux de chaque auteur et ne correspondent pas nécessairement à ceux de la Society of Actuaries, des rédacteurs du bulletin ou des employeurs des auteurs..
Bryon Robidoux, FSA, CERA, est vice-président adjoint du développement des produits auprès de Constellation Insurance. Vous pouvez le joindre bryon_robidoux@ConstellationInsurance.com.
Notes de fin de document :
[1] George E. Mobus et Michael C. Kalton. Principles of Systems Science. Springer, 2015.
[2] John H. Miller et Scott E. Page. Complex Adaptive Systems an Introduction to Computational Models of Social Life. Princeton University Press, 2007.
[3] George E. Mobus et Michael C. Kalton. Principles of Systems Science. Springer, 2015.
[4] Nair, Jayakrishnan, et al. The Fundamentals of Heavy Tails: Properties, Emergence, and Estimation. Cambridge University Press, 2022.
[6] John H. Miller et Scott E. Page. Complex Adaptive Systems an Introduction to Computational Models of Social Life. Princeton University Press, 2007.
[8] Nassim Nicholas Taleb, The Black Swan: The Impact of the Highly Improbable. Random House, 2016.
[9] Benoit B. Mandelbrot et Richard L. Hudson. The (Mis)Behavior of Markets: A Fractal View of Financial Turbulence. Basic Books, 2008.
[10] Paul Fieguth, Introduction to Complex Systems: Society, Ecology, and Nonlinear Dynamics. SPRINGER, 2021.
[12] Melanie Mitchell, Complexity: A Guided Tour. Oxford University Press, 2011.
[13] John H. Miller et Scott E. Page. Complex Adaptive Systems an Introduction to Computational Models of Social Life. Princeton University Press, 2007.
[14] George E. Mobus et Michael C. Kalton. Principles of Systems Science. Springer, 2015.
[15] Bryon Robidoux, "Adam Smith and Evolutionary Economics," The Actuary, avril 2024.
[16] Steve Keen, Debunking Economics: The Naked Emperor Dethroned? Bloomsbury Academic & Professional, 2011.
[17] Adam Smith and Evolutionary Economics
[18] Jason Potts, The New Evolutionary Microeconomics: Complexity, Competence and Adaptive Behaviour. Elgar, 2000.
[19]Fundamentals of Ecosystem Science. Elsevier Science Publishing Co Inc, 2012.
[20] Jason Potts, The New Evolutionary Microeconomics: Complexity, Competence and Adaptive Behaviour. Elgar, 2000.
[21] Damon Centola Change: How to Make Big Things Happen. John Murray, 2022.
[24] Robert B. Litterman, Investment Management: An Equilibrium Approach. J. Wiley, 2003.
[26] Philip Fernbach et Steven A. Sloman, The Knowledge Illusion: Why We Never Think Alone. Riverhead Books, 2018.
[27] Damon Centola Change: How to Make Big Things Happen. John Murray, 2022.
[28] Jason Potts, The New Evolutionary Microeconomics: Complexity, Competence and Adaptive Behaviour. Elgar, 2000.
[29] Steve Keen, Debunking Economics: The Naked Emperor Dethroned? Bloomsbury Academic & Professional, 2011.