Défis relatifs à la gestion du risque de taux d’intérêt : Partie 2—Comment tirer le meilleur parti de l’actif et du passif d’une société
par Dariush Akhtari
Gestion du risque, mai 2024

Il semble exister des points d’inflexion dans la valeur d’un instrument en cas de variation des taux d’intérêt. Ces points d’inflexion pourraient influer sensiblement sur l’approximation de la variation de la valeur effectuée à l’aide des mesures de la gestion de l’actif-passif (GAP). Dans la présente partie de la série multipartite, je présenterai :
- la façon de déterminer les points d’inflexion;
- la fourchette des variations de taux lorsque l’on peut se fier aux mesures de la GAP, c.-à-d. la fourchette de « validité », à l’extérieur de laquelle un nouveau calcul des mesures de la GAP est requis, et le besoin éventuel de rééquilibrer le portefeuille;
- une technique permettant d’améliorer l’approximation de la variation de la valeur au-delà de la fourchette de validité;
- une technique pour convertir la variation non linéaire de la courbe de rendement à utiliser avec la duration et la convexité.
Dans les prochaines parties, je vous présenterai les principales mesures de taux, leurs avantages, leurs limites, les pièges existants concernant la façon dont elles sont calculées et utilisées, et enfin, une technique pour améliorer leur utilisation.
Comment traiter les points d’inflexion
Dans le graphique portant sur la valeur d’un instrument par rapport au mouvement parallèle des taux d’intérêt, il existe des points où la taille de la convexité qui précède et suit immédiatement ce point est sensiblement différente. Je désigne ces points comme des points d’inflexion. Pour examiner cette question, nous utiliserons un portefeuille renfermant deux contrats de placement garanti (CPG) qui présentent les caractéristiques suivantes. Un contrat est assorti d’un taux de garantie minimum de 2 % et d’un bénéfice attendu de 1,5 %, tandis que l’autre est un CPG avec un taux de garantie minimum de 3 % et un bénéfice attendu de 2 %. Au départ, cinq cents dollars sont investis dans chacun d’eux et ils ont chacun une valeur de rachat partielle de 10 % par année et ils prévoient le rachat complet à la 30e année. Le graphique du contrat pour diverses courbes au comptant à points plats est illustré à la figure 1. J’utilise une courbe au comptant à points plats pour cette illustration, de même que « des mesures » pour désigner les mesures de la GAP, DV01 et CV01.
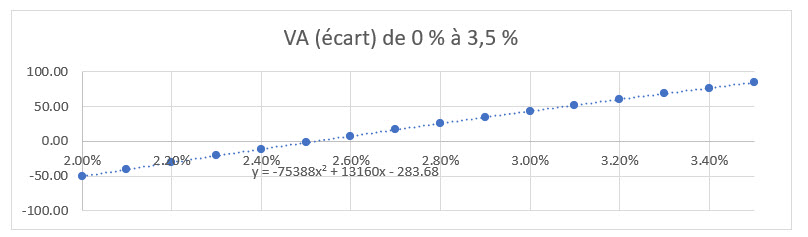
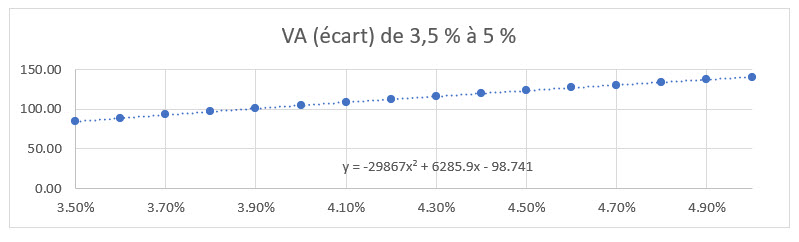
À partir des caractéristiques du produit, on s’attend à ce que la convexité du graphique change à 3,5 % (garantie minimale de 2 % + marge bénéficiaire de 1,5 %), comme on peut le voir à la figure 1, et à 5 % (3 % + 2 %). La comparaison du coefficient de x2 dans le graphique ajusté à la VA(bénéfices) en deçà de 3,5 % par rapport à celui ajusté à 3,5 % à 5 % indique que la convexité du dernier graphique, tout en ayant le même signe, représente environ 40 % de celle du premier graphique. Il est donc possible que les mesures calculées ne fournissent pas d’approximations raisonnables pour les valeurs qui recoupent les points où les mesures (en particulier la convexité) affichent une variation importante.
Figure 1
VA des écarts et de la courbe ajustée avant et après 3,5 %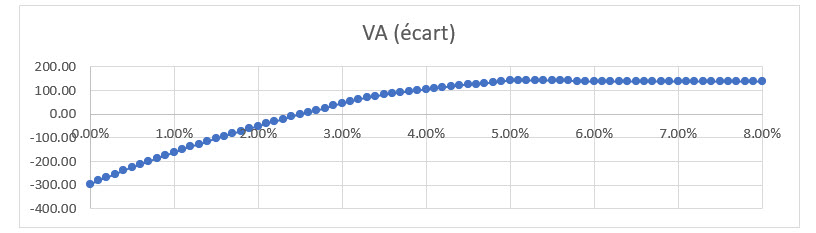
Comment identifier ces points
Puisque la convexité est la cause, nous devons la calculer à diverses variations de taux pour une fourchette à l’intérieur de laquelle nous nous attendons à ce que les taux évoluent et déterminer où change la convexité. Cela nous permettra d’être mieux outillés pour accorder notre confiance à notre approximation ou du moins être en mesure d’effectuer certains ajustements pour tenir compte de l’inexactitude du recours aux mesures à la valeur nominale. Il est facile de calculer la convexité pour les exemples simples ci-dessus à l’aide d’une courbe au comptant à points plats. Toutefois, de nombreux produits d’assurance nécessitent des simulations de modèles stochastiques fondées sur des milliers de scénarios, et il n’est pas possible d’exécuter plusieurs simulations pour déterminer la variation de valeur applicable à d’importants changements de taux.
L’objectif consiste à calculer DV01 et CV01 à l’aide de variations de 1, 5 ou 10 pb aux taux au comptant pour une fourchette de quelque -100 pb à +100 pb, et ensuite utiliser le ratio de convexités consécutives pour identifier un changement important. Il convient de noter qu’avec des variations d’un point de base (option recommandée), il faut 200 ensembles de scénarios stochastiques. Cependant, le calcul de ce nombre d’ensembles de scénarios stochastiques nécessite une longue période de simulation. On pourrait remplacer les simulations stochastiques par la combinaison de simulations déterministes à l’aide du taux au comptant à la date d’évaluation et l’écart ajusté en fonction des options (EAO). L’EAO d’un instrument représente l’écart fixe sur la courbe au comptant qui assimile la valeur actualisée (VA) de ce qui est mesuré (généralement les flux de trésorerie ou les bénéfices) à l’aide d’un scénario déterministe (généralement la courbe au comptant ou à terme) à celle produite de façon stochastique. Nous utiliserions DV01 et CV01 à l’aide de ces simulations déterministes pour ajuster les valeurs véritables de DV01 et CV01 calculées par les simulations stochastiques pour la variation attendue des taux lorsqu’une estimation est nécessaire.
Approche simple : Supposons que l’EAO ne change pas pour une variation de +/-100 pb sur la courbe au comptant
Calculons la VA de la mesure visée (flux de trésorerie ou bénéfices) à l’aide de la courbe au comptant avec les niveaux de variation souhaités de -100 pb à +100 pb. Il convient de noter que pour le calcul de la VA, l’EAO serait ajouté à la courbe au comptant en plus de toute variation. Calculons DV01 et CV01 à chaque taux varié et prenons le ratio des CV01 consécutifs. Lorsque ce ratio s’écarte sensiblement de 100 %, c’est là que se produit un point d’inflexion, et il pourrait indiquer le moment où l’approximation des variations de taux qui croisent de tels points pourrait ne pas fournir un résultat précis. Toutefois, on peut améliorer l’approximation en faisant bifurquer la variation du taux au niveau qui part du taux actuel et se rend aux taux où la convexité modifie la partie restante. Puis, l’approximation de la première partie applique des mesures à la date d’évaluation avec le montant de la variation des taux dans la première partie, et la deuxième partie de l’approximation utilise les mesures calculées à un point suivant immédiatement les changements de convexité pour la deuxième partie avec la portion restante de la variation des taux. Un exemple présenté à l’annexe 1 clarifie cette démarche et il met davantage en évidence l’approche et son efficacité.
Approche plus complexe : Supposons que l’EAO change pour une variation de +/-100 pb sur la courbe au comptant
La plupart des sociétés produisent probablement des valeurs, à des fins de gestion des risques, en utilisant des variations de +/-100 pb. Même si ces simulations ne sont pas effectuées, il est recommandé de les ajouter aux valeurs calculées actuelles. Au moyen de simulations stochastiques, l’EAO peut être calculé pour la courbe au comptant – 100 pb, à la courbe au comptant, et pour la courbe au comptant +100 pb. Appelons-les EAO-, EAO et EAO+. Calculons les valeurs actualisées comme dans l’approche simple précédente, sauf qu’au lieu d’un EAO uniforme, pour les variations négatives, utilisons l’EAO interpolé dérivé de l’EAO- et de l’EAO, et pour les variations positives, utilisons l’EAO interpolé dérivé de l’EAO et de l’EAO+.
Puisque les taux au comptant ne se déplacent pas en parallèle, il faut convertir la variation aux taux au comptant en une seule variation qui sera utilisée avec les mesures. Pour calculer cette variation des taux, la moyenne pondérée de la variation du taux au comptant peut être utilisée à l’aide de la contribution de la VA de chaque flux de trésorerie à la valeur, comme l’illustre l’annexe 2. Il est fortement recommandé d’ajouter cette approche plus complexe à tous les travaux de GAP en plus de déterminer les points d’inflexion des variations de taux qui se produiront pour le portefeuille.
Annexe 1
Examinons l’exemple présenté à la section 1. Le portefeuille se compose de deux CPG de 500 $ chacun au départ, l’un assorti d’un taux de garantie minimal de 3 % et d’une marge bénéficiaire prévue de 2 % et l’autre avec un taux de garantie minimal de 2 % et une marge bénéficiaire prévue de 1,5 %. Chaque CPG retire partiellement 10 % de la valeur de son compte par année et il est entièrement racheté après 30 ans. Supposons que le taux au comptant actuel est de 3 % et que nous souhaitons estimer la valeur de ce portefeuille à 2,5 %, 3,3 % et 3,8 %. À l’aide de la courbe au comptant à points plats, la valeur de la VA des bénéfices (écarts et aucune dépense) est calculée avec des variations de 10 pb. Par souci de simplicité, j’ai utilisé des variations de 10 pb, mais je recommande d’utiliser des variations de 1 pb à 2 pb.
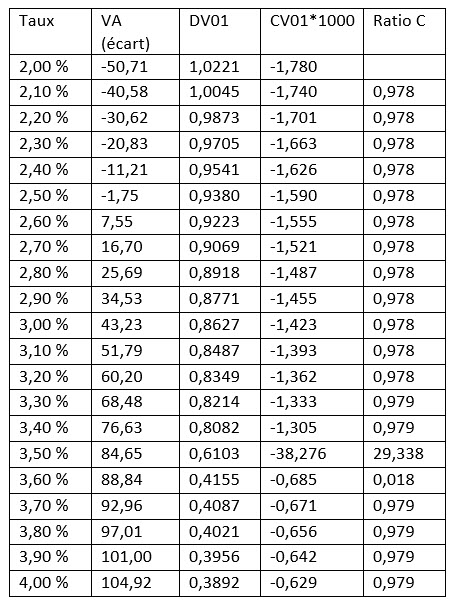
Table 1.1
Exemple de CPG simple
En examinant la colonne « Ratio C » (le ratio de la convexité en vigueur à la convexité avec une taille de variation moindre), nous constatons un changement important à 3,5 %. Cela signifie donc que nous devrons peut-être faire preuve de prudence dans notre approximation de la valeur à 3,8 %, car elle est d’un point supérieure à 3,5 %. Au départ, nous utiliserons la formule ci-dessous pour obtenir une valeur approximative.
Valeur approximative à x % = VA à 3 % + DV01 * variation + CV01 / 2 * variation2, où la variation en points de base = 10 000 * (x % - 3 %)
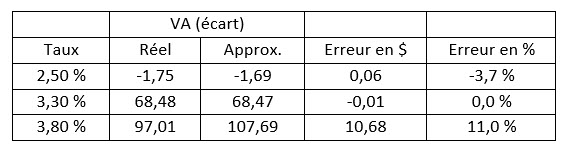
Table 1.2
Exemple de CPG simple
Comme prévu, une approximation de 3,8 % produit une erreur importante que nous n’aurions pas repérée si nous avions calculé ces valeurs à l’aveugle. Toutefois, nous savons qu’il y a un changement de convexité à 3,5 %. Donc, pour calculer la valeur à 3,8 %, nous scinderions le calcul en deux parties. La première est de 3 % à 3,5 %, et la seconde, de 3,5 % à 3,8 %. Pour la première partie, nous utiliserions des mesures à 3 % pour calculer la valeur à 3,5 %, puis nous aurions recours à des mesures à 3,6 % (une mesure calculée immédiatement après 3,5 %) pour déterminer la variation de la valeur de 3,5 % à 3,8 %.
À 3,5 %, cela se traduira par une valeur approximative de 84,59 (= 43,23 + 0,8627 * 50 – 0,001423 / 2 * 502) ) à laquelle nous devons ajouter 12,16 (= 0,4155 * 30 – 0,000685 / 2 * 302) pour les 30 pb supplémentaires de 3,5 % à 3,8 % en utilisant DV01 et CV01 à 3,6 % pour obtenir le total de 96,74. L’erreur en dollars devient -0,27 (= 96,74 – 97,01) et l’erreur en pourcentage devient -0,3 % (= -0,27 / 97,1), ce qui représente évidemment une amélioration considérable par rapport à l’approximation à l’aveugle.
Il convient de noter que dans cet exemple, j’ai simplement utilisé des simulations qui ne nécessitaient pas de calculs stochastiques. Dans la pratique, surtout lorsque les mesures sont calculées à l’aide de simulations stochastiques, les étapes ci-dessous pourraient s’appliquer.
- Calculons la valeur de l’instrument en utilisant des scénarios stochastiques.
- Calculons la valeur de l’instrument en utilisant l’espérance centrale des scénarios stochastiques, y compris tout écart supplémentaire utilisé, EC, scénario.
- Calculons l’écart ajusté des options, l’EAO, qui assimile la valeur actualisée en utilisant EC + EAO à celle calculée à l’étape 1.
- Calculons DV01 et CV01 en utilisant des simulations stochastiques représentées par « s » en exposant.
- Calculons la valeur 201 de l’instrument en exécutant des scénarios déterministes à EC + EAO et en ajoutant des variations de 1 pb de -100 pb à +100 pb (il convient de noter qu’il s’agit de simulations déterministes).
- Calculons DV01 et CV01 à diverses variations, comme cela a été fait au tableau 1.1, désigné par « d » en exposant.
- Effectuons l’approximation comme il a été expliqué ci-dessus en reconnaissant où le point d’inflexion peut se produire.
Si nous calculons la SV à +/-100 pb, dans ce qui précède, l’EAO correspondrait à l’EAO interpolé à partir de l’EAO et des valeurs calculées à des variations de +/-100 pb.
Le calcul de l’approximation jusqu’au point d’inflexion utilise des mesures avec « s » en exposant, tandis que les approximations au-delà de ces points nécessitent l’ajustement ci-dessous pour tenir compte du fait que les mesures calculées à l’aide de la simulation déterministe ne sont pas identiques à celles fondées sur des simulations stochastiques :
où ![]() représente la mesure après le point d’inflexion utilisé. Il convient de noter que
représente la mesure après le point d’inflexion utilisé. Il convient de noter que ![]() est la mesure sans variation, mais en fonction de la simulation déterministe reposant sur l’EAO (c.-à-d. la mesure à 3 % dans l’exemple ci-dessus).
est la mesure sans variation, mais en fonction de la simulation déterministe reposant sur l’EAO (c.-à-d. la mesure à 3 % dans l’exemple ci-dessus).
Annexe 2
Pour établir une approximation de la valeur d’un instrument pour une courbe de taux différente, il faut quantifier une variation de niveau. Étant donné que les taux d’intérêt ne se déplacent habituellement pas en parallèle, l’approche ci-dessous devrait être utilisée.
La variation parallèle équivalente des taux (au comptant) correspond à la moyenne pondérée du changement du taux au comptant en utilisant la contribution de la valeur actualisée de chaque flux de trésorerie à la valeur, comme l’illustre la formule ci-dessous.
![]() où Si est le taux au comptant à la période i, Δsi est la variation du taux au comptant à i et CFi est le flux de trésorerie à i. Il convient de noter que lorsqu’on utilise des produits sensibles aux taux d’intérêt, la valeur des produits doit être remplacée par CE + OAS et les CF sont ceux de la simulation déterministe utilisant CE.
où Si est le taux au comptant à la période i, Δsi est la variation du taux au comptant à i et CFi est le flux de trésorerie à i. Il convient de noter que lorsqu’on utilise des produits sensibles aux taux d’intérêt, la valeur des produits doit être remplacée par CE + OAS et les CF sont ceux de la simulation déterministe utilisant CE.
Les faits énoncés et les opinions formulées dans le présent document sont ceux de chaque auteur et ne correspondent pas nécessairement à ceux de la Society of Actuaries, des rédacteurs du bulletin ou des employeurs des auteurs.
Dariush Akhtari, FSA, FICA, MAAA, est actuaire en chef chez Converge RE. On peut le joindre à l’adresse dakhtari@converge-re.com.