Défis relatifs à la gestion du risque de taux d’intérêt : Partie 4—Comment tirer le meilleur parti de l’actif et du passif d’une société
par Dariush Akhtari
Gestion du risque, septembre 2024

Cette partie soulignera le fait que la somme des indicateurs de taux clés ne correspond pas aux indicateurs dérivés par un décalage parallèle de l’ensemble de la courbe, même pour des tailles de décalage très faibles, et comment définir un changement de taux unique à appliquer à un taux clé (ou à la courbe en entier), étant donné que les variations de taux ne sont généralement pas uniformes ni parallèles.
Dans la prochaine partie, j’évaluerai diverses méthodes utilisées pour contrer la non-additivité des taux clés.
Non-additivité des taux clés
Précédemment, j’ai indiqué que pour les instruments sensibles aux taux d’intérêt, l’utilisation de plus petites tailles de décalage produit des KRkDV01s dont la somme est beaucoup plus proche de DV01, alors que ce n’est pas le cas des tailles de décalage plus importantes. Cela est dû à deux raisons principales. Premièrement, avec des tailles de décalage plus importantes, les variations de taux plus élevées peuvent déclencher des variations de flux de trésorerie, ce qui entraîne une interaction plus importante entre les taux clés. Deuxièmement, il est plus probable qu’un des taux faisant l’objet d’un décalage traverse un point d’inflexion.
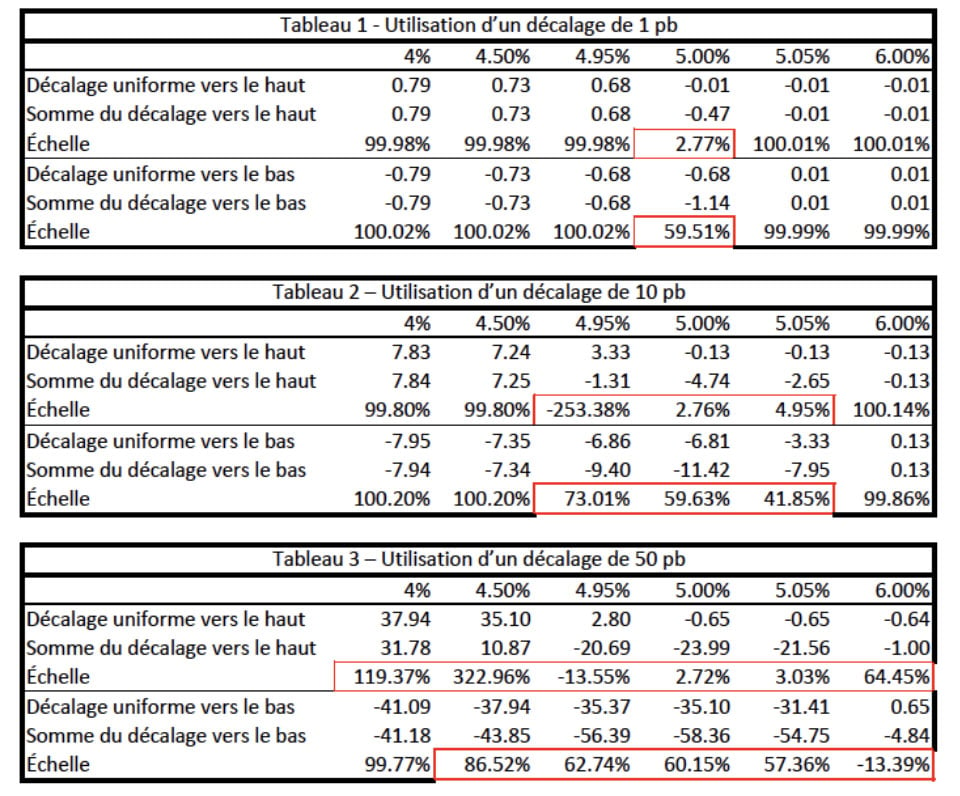
Pour explorer la mesure dans laquelle la somme des KRkDV01s se rapproche de DV01, nous pourrions utiliser une échelle pour comparer le ratio de DV01 à la somme des KRkDV01s, ou de façon plus appropriée, à leurs sous-composantes, c.-à-d. les valeurs utilisant des tailles de décalage plus élevées et moins élevées. Évidemment, plus l’échelle se rapproche de 100 %, plus la somme des KRkDV01s se rapproche de DV01. La valeur se rapprochera beaucoup plus de 100 % lorsque la taille de décalage est de 1 point de base (pb), mais sera très faible (disons 2 %) ou très élevée (disons 400 %) lorsqu’un décalage de 50 pb est utilisé. En fait, plus on se rapproche du point d’inflexion, plus la valeur d’échelle s’éloignera de 100 %. Les tableaux 1, 2 et 3 de la figure 1 soulignent l’incidence de diverses tailles de décalage sur ce ratio (c.-à-d. le ratio de la variation de la valeur attribuable à l’application d’un décalage uniforme vers le haut/bas à la courbe en entier par rapport à la somme des variations de la valeur lorsque la même taille de décalage est appliquée à certaines parties de la courbe pour l’obtention de taux clés). Le problème est exacerbé à mesure que l’on se rapproche du point d’inflexion et que la taille du décalage prend de l’ampleur.
Figure 1
Tableaux 1 à 3 : Incidence sur l’échelle de la variation de la taille du décalage sur la courbe
D’après les tableaux de la figure 1, on peut remarquer que les tailles de décalage plus élevées et la proximité du point d’inflexion font en sorte que l’échelle s’éloigne sensiblement de 100 %. L’approche présentée dans la partie 2 de la présente série d’articles peut également être appliquée aux taux clés pour déterminer le niveau de variation des taux dont on pourrait se fier pour déterminer la validité approximative des taux clés. De plus, l’utilisation du calcul cumulatif des taux clés tient compte des taux croisés et améliorerait les approximations à l’aide des taux clés.
Comment calculer la variation de taux à appliquer aux mesures
Pour utiliser les mesures de la GAP, il faut savoir à quel point les taux ont changé. J’ai comparé trois approches différentes.
Moyenne des variations de taux
Cette approche prend simplement la moyenne de toutes les variations de taux au cours de la période utilisée. Par exemple, pour le taux directeur 5, la moyenne des variations de taux au cours des années deux à 10 serait utilisée et, dans un cas parallèle, la moyenne des variations de taux sur l’ensemble de la courbe serait utilisée. Selon cette approche, toutes les périodes ont une pondération équivalente.
Variation de rendement calculée
On pourrait convertir l’ensemble de la courbe des taux au comptant en fonction du rendement, en calculant un taux de rendement interne (TRI) des flux de trésorerie à leur valeur actualisée. De même, après un changement de taux, on pourrait calculer le rendement en prenant le TRI des mêmes flux de trésorerie à leur valeur actualisée au moyen des nouveaux taux. La variation de ce rendement par rapport aux données d’origine représente la variation à utiliser pour ce taux clé. Notez que l’on pourrait toujours considérer l’ensemble de la courbe comme étant un taux clé important.
Variation des taux pondérés (approche proposée)
Pour tenir compte de la pondération inégale d’un flux de trésorerie sur la valeur actualisée, je propose de pondérer la variation de taux pour chaque période en fonction du ratio de la valeur actualisée des flux de trésorerie de cette période à la valeur totale, comme expliqué à l’annexe 1.
Comparaison des méthodes de variation des taux
J’ai comparé l’erreur absolue de la valeur approximative en utilisant un décalage de 1 pb pour la variation et en l’appliquant à la courbe entière (c.-à-d. en utilisant DV01 et CV01) pour les cas A (qui seront définis à la partie 5), comme le montre le tableau 4. Comme on peut le constater au tableau 4, l’approche fondée sur les flux de trésorerie pondérés semble surpasser les autres approches en ce qui a trait au calcul d’une variation de taux unique à utiliser pour l’établissement du taux clé.
Tableau 4
Comparaison de diverses méthodes de variation des taux sur la courbe entière
Annexe 1
Voici la pondération recommandée utilisée pour comprimer la variation des taux au cours des périodes visées par un taux clé en un taux unique applicable à KRkDV01 et KRkCV01. On suggère aussi d’appliquer cette méthode à la variation de la courbe des taux au comptant en entier pour DV01 et CV01. Pour calculer un décalage pondéré, il faut tenir compte du tableau A1.1.
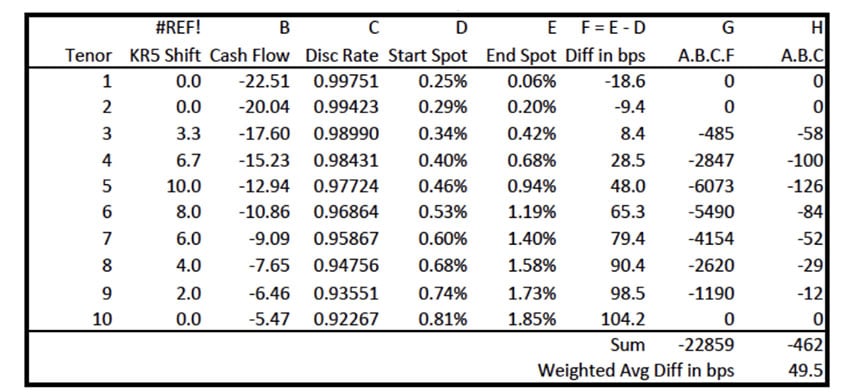
La colonne A représente le décalage appliqué au taux clé particulier (KR 5 dans l’exemple ci-dessous, en utilisant un décalage de 10 pb). La colonne B représente les flux de trésorerie calculés en utilisant les taux au comptant au début de la période (c.-à-d. la colonne D). La colonne C représente le taux d’actualisation (taux d’actualisation (t-1) / (1+taux au comptant (t) dans D) qui, lorsqu’il est appliqué aux flux de trésorerie et additionné, produirait la valeur de l’instrument. La colonne E représente les taux au comptant pour la période où la valeur de l’instrument doit être établie par approximation. La colonne F représente simplement la différence entre les colonnes E et D. La colonne G est le produit des colonnes A, B, C et F. La colonne H est le produit des colonnes A, B et C. Enfin, la moyenne pondérée des taux utilisés avec le taux clé visé est le ratio des sommes des colonnes G et H.
En examinant la colonne F, il aurait été difficile de choisir un taux unique à utiliser avec KR5DV01/KR5CV01. Selon cette méthode et pour cet ensemble de flux de trésorerie, il faudrait appliquer un décalage de 49,5 points de base pour le taux directeur 5.
Tableau A1.1
Comment calculer la variation de taux pondérée
Les faits énoncés et les opinions formulées dans le présent document sont ceux de chaque auteur et ne correspondent pas nécessairement à ceux de la Society of Actuaries, des rédacteurs du bulletin ou des employeurs des auteurs..
Dariush Akhtari, FSA, FICA, MAAA, est actuaire en chef auprès de Converge RE. Vous pouvez le joindre à dakhtari@converge-re.com.