Quantification et évaluation de la juste valeur des rentes à terme fixe indexées

par Peter M. Phillips et Tao Wang
Gestion du risque, Février 2022

L’Accounting Standards Update (ASU) 2018-12 (intitulée « Targeted Improvements to the Accounting for Long-Duration Contracts ») publiée par le Financial Accounting Standards Board (FASB) des États-Unis vise à améliorer les exigences de divulgation en vertu des principes comptables généralement reconnus (PCGR) des États-Unis pour certains contrats de longue durée, y compris les rentes à terme fixe indexées (RTFI). L’un des domaines d’intérêt de l’ASU 2018-12 est la déclaration d’une nouvelle classification des passifs au titre de la prestation fondée sur le risque de marché (PRM), qui doit être évaluée d’une manière conforme au marché d’après les exigences de comptabilisation des améliorations ciblées aux contrats de longue durée (ACCLD, ndlt : long-duration targeted improvements (LTDI)). Les avenants de prestation minimale garantie de prestations du vivant et ceux de prestations minimales garanties de décès offerts dans des RTFI sont habituellement évalués et déclarés à l’aide de scénarios risques-neutres.

Par coïncidence, l’ébauche du cadre des provisions fondées sur des principes (PFP) pour les RTFI (VM-22, ndlt: Valuation Manual 2022) proposée par la National Association of Insurance Commissioners (NAIC) introduit une composante de réserve stochastique semblable à celle requise par le cadre VM-21 pour les produits de rentes variables. La transition du cadre déterministe actuel au cadre VM-22 représente un défi pour de nombreuses sociétés d’assurances, mais elle permet aussi de mesurer et de gérer de façon plus uniforme les risques liés aux RTFI.

Dans le présent article, deux méthodes d’évaluation des RTFI couramment utilisées sont comparées numériquement pour aider les sociétés d’assurances à déterminer la meilleure méthode à utiliser en vertu des normes des ACCLD et du cadre VM-22 (PCGR). Nous avons comparé deux approches de modélisation pour projeter les contrats à terme sur indice boursier à l’aide de la formule annuelle de crédit point à point : le modèle stochastique de crédit sur actions et le modèle déterministe de crédit du budget des options. L’analyse est ensuite appliquée aux différents niveaux des budgets des options et à la formule mensuelle moyenne des crédits. Les avantages et les inconvénients des deux approches de projection du rendement des actions sont également soulignés et seront abordés plus loin dans le rapport.

Nous concluons que le modèle stochastique de crédit sur actions est davantage à même de saisir la juste valeur des avenants liés aux RTFI pour les deux méthodes de crédit et les différents paramètres des hypothèses. L’évaluation des garanties incorporées fait appel à des mathématiques complexes et nécessite des simulations stochastiques sur stochastiques sophistiquées. Le modèle déterministe de crédit du budget des options est une approche abrégée qui peut produire des écarts importants dans certaines situations comparativement au modèle stochastique plus robuste de crédit sur actions. En outre, le modèle de crédit du budget des options produit une meilleure estimation unique plutôt qu’une distribution requise aux fins du calcul des provisions et de la gestion des risques liée aux PFP.

Approches, données et hypothèses

Deux approches sont couramment utilisées pour projeter les crédits indiciels : le modèle stochastique de crédit sur actions et le modèle déterministe de crédit du budget des options.

• Modèle stochastique de crédit sur actions. Ce modèle nécessite un modèle stochastique de simulation des actions étalonné sur le marché pour générer un grand nombre de scénarios de titres dans des conditions risques-neutres. L’algorithme calcule également le prix des options (avec des prix d’exercice différents) pour chaque scénario simulé. En fonction de ces prix et du niveau du budget des options disponibles, nous pouvons calculer le taux de plafonnement, le taux de participation et l’écart de l’indice qui en résultent. Ces paramètres sont réinitialisés au début de chaque année et ils demeurent constants tout au long de l’année. Après avoir appliqué les paramètres à la variation de l’indice, nous obtenons le rendement indexé selon le modèle stochastique de crédit sur actions. Ce modèle est sophistiqué et il nécessite un modèle de simulation et des ressources informatiques de pointe.
• Modèle déterministe de crédit du budget des options. Ce modèle est un raccourci qui ne nécessite pas la simulation du rendement des actions. Le crédit de la valeur du compte repose simplement sur le niveau du budget des options disponibles. Au début de chaque année, le modèle enregistre le niveau du budget des options disponibles et il le cumule ensuite aux taux sans risque au cours de l’année. Pour qu’il soit comparable au modèle stochastique de crédit sur actions, le taux crédité ne chute pas sous un taux plancher qui correspond au taux plafond minimum, et le taux plancher est adossé à la formule de Black-Scholes. Il s’agit d’une approche simple et rapide. Cette approche présente un inconvénient immédiat : elle ne tient pas compte de la distribution complète des résultats aux fins de gestion du risque extrême et de calcul des provisions mathématiques.

Pour déterminer l’approche la plus à même de saisir la juste valeur de la PRM, nous avons comparé les résultats selon quatre modèles différents, du plus simple (modèle déterministe de crédit du budget des options avec modèle déterministe de taux d’intérêt) au plus complexe (modèle stochastique de crédit sur actions avec modèle stochastique de taux d’intérêt), comme le montre le tableau 1.

Tableau 1
Spécification du modèle d’évaluation selon la PRM

Pour les simulations relatives aux actions risque-neutres, le modèle de Bates est utilisé. Comparativement au cadre traditionnel de Black-Scholes, le modèle de Bates est capable de simuler à la fois des volatilités stochastiques et des sauts stochastiques. Le modèle de Bates est l’un des modèles sophistiqués de risque de marché utilisés aujourd’hui par les sociétés d’assurances offrant des RTFI. Pour les simulations de taux d’intérêt, le modèle de taux court à deux facteurs de Hull-White (HW2F) est utilisé pour saisir les mouvements non parallèles de la courbe de rendement et il peut produire une structure temporaire plus réaliste de la volatilité des taux d’intérêt. Dans notre analyse, les deux modèles ont été étalonnés en fonction du contexte actuel des marchés financiers pour produire des résultats conformes au marché.

Pour établir le niveau du budget des options disponibles, nous suivons la pratique courante consistant à calculer la différence entre le rendement du compte général et l’écart de prix requis. Les rendements du compte général sont simulés. Toutefois, l’écart de prix requis est une hypothèse plus subjective, car elle dépend de l’attente de rentabilité de la société d’assurances. Par conséquent, afin de maintenir notre impartialité, nous avons effectué des comparaisons des résultats sur différents niveaux d’écarts de prix requis.

La déchéance dynamique est également un risque important à prendre en compte dans l’analyse des RTFI. L’incitatif de rachat pour un titulaire dépend du point d’écart par rapport au prix d’exercice d’une police. On suppose qu’un titulaire compare rationnellement la valeur actualisée des prestations attendues à la valeur de rachat lorsqu’il prend des décisions de rachat. Lorsque la valeur de rachat est suffisamment supérieure à la valeur actualisée des prestations attendues, le titulaire a un incitatif plus élevé pour résilier la police. Le taux de déchéance dynamique varie selon les différents scénarios simulés de taux d’intérêt et de rendement des actions.

Une autre considération importante dans cette analyse est le niveau du budget des options disponibles. Celui-ci peut être modélisé à titre de différence entre le rendement du compte général et l’écart de prix requis. Le rendement du compte général dépend du rendement d’un portefeuille de placements désigné qui est principalement composé d’actifs à revenu fixe. L’écart de prix requis est fixé par les sociétés d’assurances pour répondre aux exigences de rentabilité. Dans les limites du budget des options disponibles, les sociétés d’assurances appliquent habituellement une stratégie annuelle pour couvrir les garanties de taux crédités. Les paramètres des options sont réinitialisés chaque année, compte tenu de la fluctuation du prix des options et du rendement du compte général.

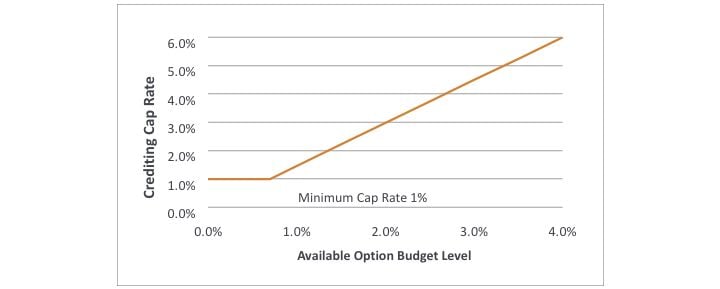
Avec un budget d’options plus élevé, le plafond du rendement indexé peut être relevé, comme l’illustre la figure 1. Lorsque le niveau du budget d’options disponibles est inférieur à un certain seuil, le taux de plafonnement demeure à son niveau minimal.

Figure 1
Taux de plafonnement par rapport au niveau du budget des options disponibles

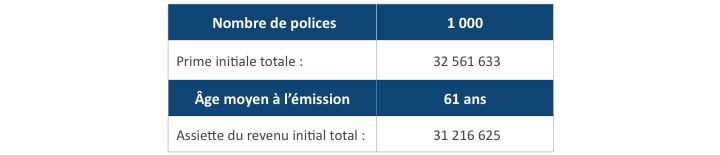
Le tableau 2 présente l’exemple du portefeuille de RTFI utilisé dans notre analyse. Toutes les polices sont assorties d’une stratégie annuelle de réinitialisation du plafond, d’une prestation garantie de retraits viagers (PGRV) et d’une prestation garantie minimale de décès (PGMD). Le taux de plafonnement pour la réinitialisation ne tombe jamais sous 1,00 %; autrement dit, le taux de plafonnement minimal est de 1,00 %. La base de prestations de l’avenant PGVR illustré comporte un cumul annuel entre 6,50 % et 7,00 % (selon l’avenant choisi par le titulaire) composé annuellement jusqu’à l’activation de la prestation. Les frais annuels de l’avenant représentent entre 0,95 % et 1,10 % de la base de prestations. Le pourcentage maximal annuel du retrait dépend de l’âge atteint du titulaire au moment de l’activation des retraits et de la question de savoir si le contrat de RTFI est une police conjointe.

Tableau 2
Profil du portefeuille des polices en vigueur

Hypothèses

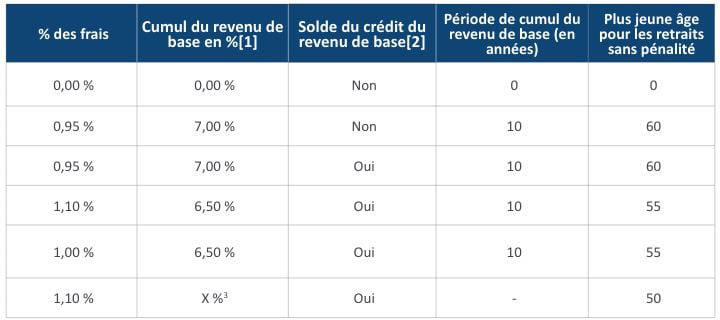
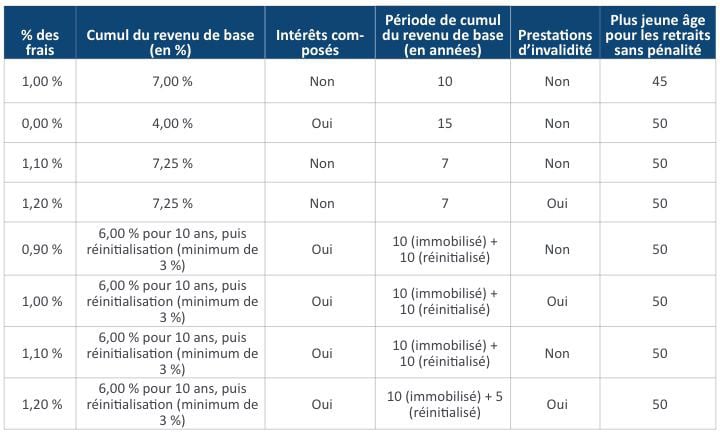
Nous avons comparé l’hypothèse des frais d’avenant figurant au tableau 3 et les observations de l’industrie présentées au tableau 4 pour nous assurer que des paramètres réalistes ont été utilisés dans notre analyse. Pour chaque police, l’un des barèmes de frais d’avenant est utilisé.

Tableau 3
Hypothèses relatives aux frais d’avenant

Notes :

1. Le cumul du revenu de base est composé annuellement.
2. Cette caractéristique offre une certaine souplesse aux titulaires de police. À l’étape du crédit du revenu de base, lorsqu’il y a un petit nombre de retraits, le revenu de base sera crédité de la différence entre le pourcentage de cumul du revenu de base et le pourcentage du retrait.
3. Si des retraits ont déjà eu lieu, taux de cumul = 1,5 x croissance de la valeur du compte. Sinon, le taux de cumul = 2,5 × la croissance de la valeur du compte.

Tableau 4
Frais d’avenant types

Analyse de base : Méthode annuelle de crédit point à point

Le crédit indexé sur la valeur du compte de la police dépend à la fois du rendement d’un indice externe (comme S & P 500®) et de la méthode de crédit choisie pour la valeur du compte. Le rendement de la valeur du compte de la police a une incidence directe sur la PRM.

La méthode annuelle point à point est le type de crédit le plus courant sur les marchés des RTFI. La variation de l’indice dépend uniquement de la différence entre le point final de l’indice boursier et son point de départ, et elle ne tient pas compte des points entre les deux. La variation de l’indice au moyen de cette méthode est calculée comme suit :

Pour obtenir le rendement indexé, un écart d’indice est déduit de la variation de l’indice et la différence est multipliée par un taux de participation qui définit la partie du gain de l’indice boursier à créditer. Le taux d’intérêt indexé est assujetti à un taux plafond et ne descend jamais sous 0 %.

La société d’assurances a le droit de réinitialiser périodiquement les paramètres de rendement indexé, qui dépendent principalement de la fluctuation du budget des options disponibles. Compte tenu des écarts de prix variables et des chocs du rendement général du compte, la performance des quatre modèles est indiquée ci-dessous.

Écart de prix de 1 %

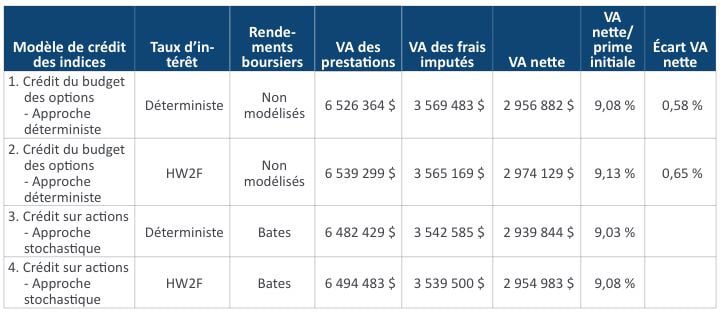
Le tableau 5 ci-après présente les résultats des quatre combinaisons de modèles présentées au tableau 1. La colonne « VA des prestations » du tableau quantifie les valeurs actuarielles actualisées du passif futur pour risque de marché de la société d’assurances à l’aide des modèles précisés à chaque ligne. La colonne « VA nette » présente le résultat à la juste valeur, c’est-à-dire la différence entre les valeurs actualisées des prestations futures et celles des frais imputés. La dernière colonne « Écart de l’approche du budget des options » compare le résultat du modèle déterministe de crédit du budget des options et du modèle stochastique de crédit du budget des options sur actions, compte tenu du même modèle de taux d’intérêt.

Tableau 5
Résultats (écart de prix = 1 %)

Notes :

• VA des prestations : Valeurs actuarielles actualisées du passif futur pour risque de marché de la société d’assurances au moyen des modèles énoncés à chaque ligne.
• VA nette : Juste valeur de la différence entre les prestations futures et les frais imputés.
• Écart de VA nette attribuable à l’approche du budget des options : Différence entre l’approche déterministe de crédit du budget des options et l’approche stochastique de crédit du budget des options sur actions selon le même modèle de taux d’intérêt :
  2 956 882 $ / 2 939 844 $ – 1 = 0,58 % et 2 974 129 $ / 2 954 983 $ – 1 = 0,65 %.

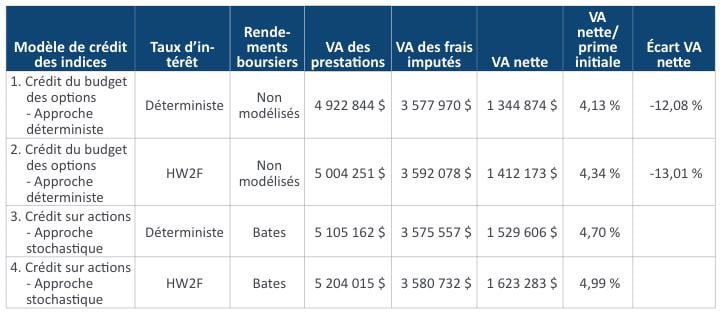
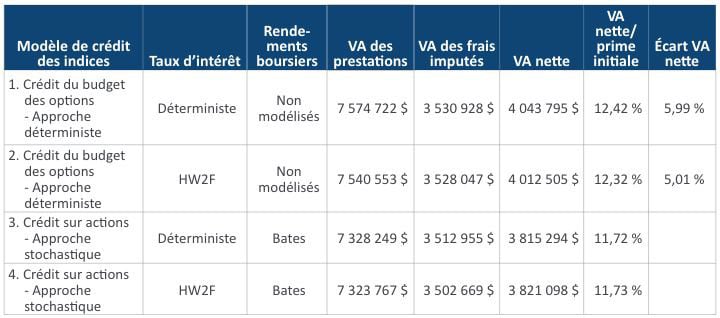
Avec un écart de prix de 1 %, il n’y a pas de différence importante entre les modèles. Toutefois, la situation change selon les différentes hypothèses de rendement du compte général. Le tableau 6 présente les résultats avec le même écart de prix, mais un déplacement parallèle des courbes de rendement du compte général en hausse de 1 %. Il prévoit un budget d’options plus élevé que dans le cas précédent et il est plausible dans un contexte de hausse des taux d’intérêt. Le modèle de crédit du budget des options selon l’approche déterministe sous-estime le passif de plus de 12 % par rapport au modèle stochastique de crédit sur actions et il ne tient pas compte de la dynamique complète des scénarios d’actions.

Écart de prix de 1 % et augmentation parallèle du rendement du compte général de 1 %

Tableau 6
Résultats (écart de prix = 1 % et augmentation du rendement du compte général de 1 %)

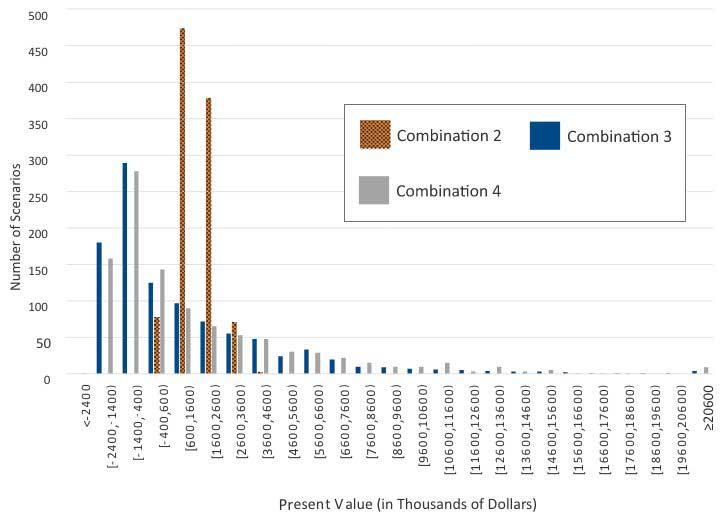
Toutes les combinaisons de modèles à l’exception de la première (un modèle déterministe de taux d’intérêt dont le rendement des actions n’est pas modélisé) peuvent produire des distributions de la valeur actualisée. La figure 2 montre les différentes distributions. Nous constatons une incidence importante du modèle de taux d’intérêt sur la distribution des valeurs actualisées. Par conséquent, la sélection des modèles est importante lorsqu’il s’agit de gérer le risque lié au produit dans une vaste gamme de scénarios, surtout les scénarios extrêmes. L’approche de modélisation déterministe est insuffisante dans ce cas.

Figure 2
Histogramme de la VA nette dans toutes les combinaisons du tableau 6

Note:

Écart de prix de 2 %

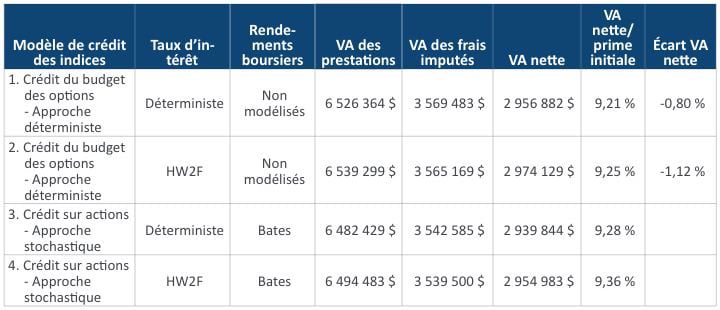
L’écart de prix peut également faire une grande différence au chapitre des résultats du modèle, comme le montre le tableau 7. Le modèle de taux d’intérêt a été étalonné en fonction des prix du marché observés en décembre 2019 lorsque le rendement des bons du Trésor américain à dix ans était inférieur à 2 %. Si la société d’assurances exige un écart de prix relativement élevé de 2 % dans un tel contexte de taux d’intérêt, le niveau du budget des options disponibles sera faible et atteindra même 0 % pour certains scénarios simulés.

Lorsque ce niveau sera de 0 %, la garantie de taux plafond minimum sera activée. Autrement dit, le taux plafond demeurera au niveau minimal de 1 %.

• Selon le modèle stochastique de crédit sur actions, la valeur du compte sera créditée au moyen d’une stratégie d’option d’écart haussier dont le plancher est de 0 % et le plafond de 1 %.
• Selon le modèle déterministe de crédit du budget des options, la valeur du compte sera portée directement au crédit du prix de cette stratégie d’option d’écart haussier. Comme il n’y a pas de simulation des actions dans ce modèle, par défaut, la tarification est produite au moyen de la formule de Black-Scholes.
  
  

Tableau 7
Résultats (écart de prix = 2 %)

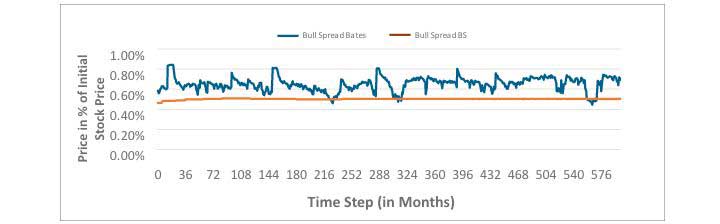
Dans ce cas, le modèle déterministe de crédit du budget des options surestime le passif de plus de 5 %. La formule de Black-Scholes ne saisit pas la nature stochastique des volatilités et des sauts. Par conséquent, elle sous-évalue la stratégie de l’option de l’écart haussier dans la plupart des scénarios. La figure 3 compare les prix simulés par le modèle de Bates et les prix de Black-Scholes selon un scénario type de taux d’intérêt.

Figure 3
Comparaison des prix de l’option d’écart haussier entre les formules de Bates et de Black-Scholes (BS)

Analyse étendue : Méthode de crédit mensuel moyen

Afin d’étudier l’incidence des différentes méthodes de calcul du crédit, la comparaison des quatre combinaisons de modèles est appliquée à la méthode de calcul des crédits mensuels moyens. Cette méthode enregistre les valeurs d’un indice boursier à la fin de chaque mois, puis utilise la moyenne de 12 valeurs consécutives de l’indice à la fin du mois pour obtenir la moyenne mobile sur 12 mois. Cette méthode permet de comparer cette moyenne mobile sur 12 mois à la valeur de l’indice au début de l’année afin de déterminer la variation de l’indice, comme il est indiqué ci-dessous.

Comparativement à la méthode annuelle de crédit point à point, cette méthode réduit la volatilité de l’indice en établissant la moyenne des valeurs de l’indice et présente un potentiel de majoration limité. Pour ce qui est de la modélisation, la nature dépendante de la trajectoire de cette méthode de crédit est plus difficile à gérer. Les rendements indexés sont déterminés d’après la même règle que dans la méthode annuelle de crédit point à point. La société d’assurances a le droit de réinitialiser les paramètres, y compris les taux plafond, les taux de participation et les écarts indiciels en fonction du budget des options disponibles.

Le tableau 8 présente les résultats avec un écart de prix de 1 %.

Tableau 8
Résultats (écart de prix = 1 %)

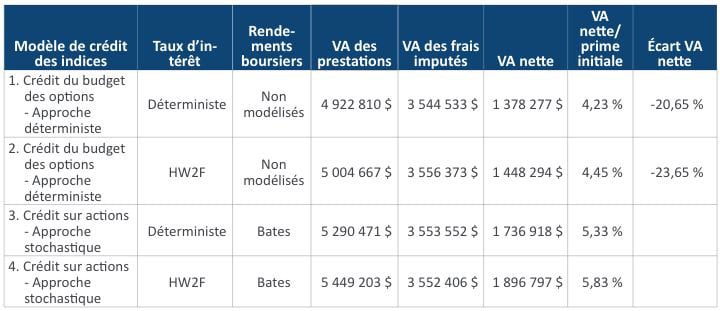
À l’instar de la méthode annuelle de crédit point à point, aucune différence importante n’est observée lorsque l’écart de prix est de 1 %. Le tableau 9 présente les résultats avec un changement parallèle de 1 % des rendements du compte général. Le modèle déterministe de crédit du budget des options sous-estime le passif de plus de 20 % par rapport à son équivalent stochastique, comme nous l’avons observé dans la méthode annuelle de crédit point à point.

Tableau 9
Résultats (écart de prix = 1 % et rendement du compte général à la hausse de 1 %)

Conclusion

Le modèle déterministe de crédit du budget des options produit une évaluation simple fondée sur la meilleure estimation et il est plus rapide à calculer. Nous avons toutefois observé que ce modèle de raccourci peut sous-estimer ou surestimer considérablement le passif des RTFI, comparativement aux modèles stochastiques qui utilisent un grand nombre de scénarios de rendement des actions conformes au marché. Il ne saisit pas non plus toute la distribution des évaluations, ce qui est important pour la gestion des risques.

Les rapports sur la PRM introduits par l’ASU 2018-12 exigent généralement que les avenants des RTFI soient déclarés à la juste valeur après les LDTI. De plus, en vertu du nouveau cadre de PFP pour les rentes fixes (VM-22), le provisionnement pour les avenants de RTFI nécessitera probablement l’utilisation d’une mesure ECU à 70. Bien qu’il soit important d’évaluer diverses approches de modélisation pour satisfaire aux nouvelles exigences réglementaires, il s’agit également d’une bonne occasion d’examiner comment les modèles peuvent aider à quantifier les risques dans les produits de RTFI.

Les faits énoncés et les opinions formulées dans le présent document sont ceux de chaque auteur et ne correspondent pas nécessairement à ceux de la Society of Actuaries, des rédacteurs du bulletin ou des employeurs des auteurs.

---

Peter M. Phillips est président et chef de la direction d’Aon PathWise Solutions Group LLC. On peut le joindre à peter.phillips@aon.com. LinkedIn.

Tao Wang, Ph. D., ASA, MAAA, est directeur général et chef des services-conseils d’Aon PathWise Solutions Group LLC. On peut le joindre à tao.wang@aon.com. LinkedIn.