Apprentissage profond en gestion des risques : Une introduction en douceur

par Damon Levine

Gestion du risque, septembre 2022

Dans le présent article, un réseau neuronal artificiel (RNA) est appliqué à un défi de risque réel. Cette introduction de haut niveau à l’apprentissage profond au moyen des RNA n’utilise que des concepts mathématiques et statistiques de base. Nous commençons par une approche de modélisation connue, puis nous l’améliorons pour qu’elle puisse « apprendre » à mieux correspondre aux données existantes et fournir (espérons-le) des projections exactes des valeurs futures.

Les types de données sont précisés dans ces exemples, mais ces méthodes fonctionnent également bien pour un très large éventail de problèmes réels et le contexte particulier est non pertinent.

Une seule « exigence » : l’ampleur de l’intérêt dépend sensiblement d’un ensemble de variables quantitatives (p. ex., les points de données historiques) de façon numérique.

Ensemble de données de formation

Dans de nombreuses situations, nous possédons des données pour des clients existants et nous voulons les utiliser pour attribuer une cote de risque à un client potentiel.

Dans l’exemple, une banque a recueilli les champs numériques suivants pour les sociétés qui sollicitent une marge de crédit ou un prêt :

• Ratio de liquidité relative : Actifs à court terme moins stocks divisés par passifs à court terme.
• Avoir au bilan.
• Ratio des flux monétaires nets mensuels aux dépenses monétaires mensuelles.
• Cote de santé financière (p. ex., cote de santé financière S&P ou cote équivalente d’une société privée).
• Cote liée à l’accès de la société à des fonds supplémentaires au moyen de marges de crédit ou d’autres sources.

Chacune de ces variables sera mise à l’échelle pour correspondre à des décimales de l’ordre de [0,1] et nous désignerons ces variables explicatives comme étant x₁, x₂, x₃, x₄, et x₅, respectivement. Supposons que nous connaissons la cote de risque, également dans la fourchette [0,1], que nous considérons comme correcte pour les clients existants. Nous voulons utiliser ces données pour produire une cote de risque pour les nouveaux clients d’affaires potentiels. Il convient de noter que (1) la mise à l’échelle peut être effectuée telle que des valeurs plus élevées correspondent à des niveaux de risque plus élevés ou plus faibles, comme le veut le modélisateur, mais ce n’est pas important pour nos besoins, et (2) la mise à l’échelle n’est pas une exigence pour aucune des techniques présentées.

Comme nous l’avons mentionné, nous disposons des données souhaitées sur les sociétés existantes et nous savons quelles cotes de risque elles auraient dû recevoir. Cela nous servira d’ensemble de « données de formation » et nous permettra d’étalonner notre modèle.

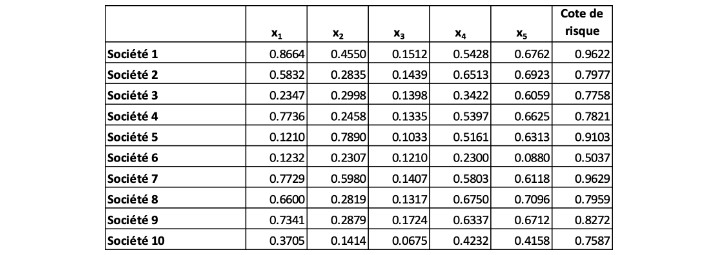
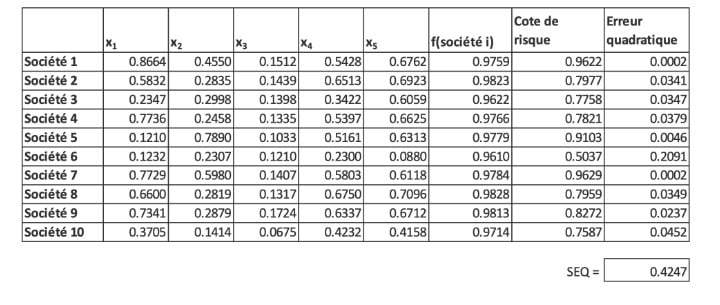
Nos données de formation, qui comprennent les variables explicatives et les cotes de risque qui leur sont associées, sont présentées ci-dessous au tableau I.

Tableau 1
Ensemble de données de formation

Une optimisation linéaire

L’objectif consiste à trouver un modèle qui attribue une cote de risque à une société en fonction de ses cinq variables de santé financière, soit x₁, x₂, x₃, x₄, et x₅. Ce modèle est « adapté » en utilisant les données du tableau I. Une approche simple consiste à supposer que la cote de risque modélisée, f, est une combinaison linéaire des variables d’intrant :

où les {w_i} sont des « facteurs de pondération » (constantes réelles) à être déterminés et nous trouvons les « meilleurs » facteurs possibles. En résumé, nous pouvons nous reporter à cette cote de risque modélisé, pour une société i, sous le nom de f (société i).

Nous cherchons les facteurs de pondération qui permettent à la fonction de bien performer dans l’ensemble de données de formation. Nous espérons que la fonction performera également bien pour les nouvelles sociétés qui ne sont pas présentes dans la formation.

Nous déterminons les valeurs des facteurs de pondération comme étant celles qui minimisent la somme des erreurs quadratiques (SEQ) :

Lorsque la somme est pour les éléments de i allant de 1 à 10, l’ensemble de formation est complet.

Les valeurs des facteurs de pondération qui minimisent la SEQ définie ci-dessus pour la fonction linéaire f sont habituellement appelées coefficients de régression, et l’optimisation proposée n’est rien de plus que la régression linéaire multiple (sans terme constant) dans l’ensemble de formation.

Pour ce faire, dans Excel, nous utilisons le module complémentaire Solver et la méthode de descente de gradient pour l’optimisation. La descente de gradient utilise essentiellement des dérivés du calcul différentiel afin d’améliorer de façon itérative les facteurs de pondération en ce qui concerne leur incidence sur la SEQ ou une autre fonction d’erreur ou de coût définie par l’utilisateur. Des détails supplémentaires sur cette approche figurent plus loin dans le présent article.

L’optimisation indique les meilleurs facteurs de pondération comme suit :

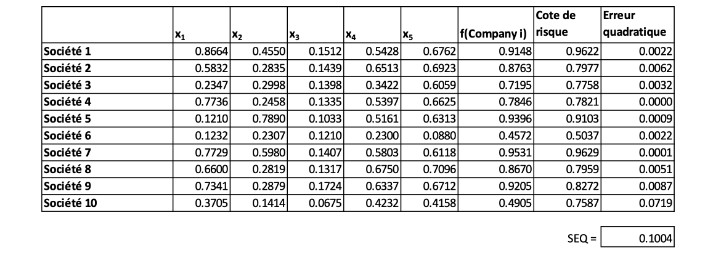
La fonction donne de bons résultats pour l’ensemble de formation, la SEQ étant égale à 0,1004, comme le montre le tableau II ci dessous.

Tableau II
Performance du modèle linéaire pour les données de formation

Comme nous l’avons mentionné, le modèle est ajusté aux données de formation; puis nous examinons la performance à l’égard de ces données ainsi que des données d’essai, qui sont un ensemble extérieur aux données de formation. En pratique, les données d’essai peuvent être un sous-ensemble de données qui étaient connues au moment de l’ajustement du modèle, mais qui ont été délibérément exclues de l’ensemble de formation. Il peut également s’agir d’un ensemble de données obtenu après cet ajustement. Dans un cas comme dans l’autre, il fournit un test décisif du modèle ajusté dans un environnement hors échantillon. Il est nécessaire que nous connaissions la valeur actuelle de la variable-réponse pour les données de formation, soit, dans ce cas, la cote de risque.

Les données d’essai sont utilisées pour avoir confiance que le modèle servira au but visé et servira de prédicteur solide lorsqu’il est utilisé avec des données « différentes ». Si un modèle ne performe pas bien avec des données d’essai, il ne peut être considéré comme un modèle solide malgré les résultats positifs obtenus à l’égard des données de formation.

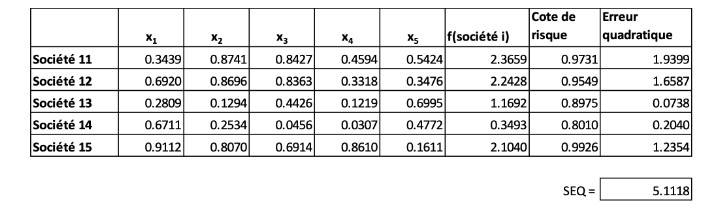
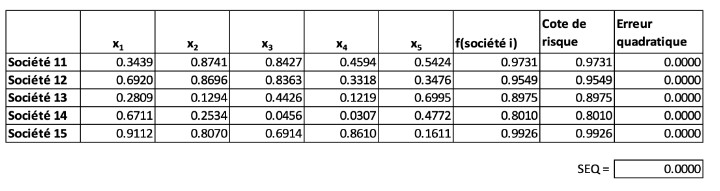
La performance par rapport à nos données d’essai, soit les sociétés 11 à 15, est moins impressionnante, comme il est indiqué ci-dessous.

Tableau III
Performance du modèle linéaire sur les données d’essai

Le modèle ne donne pas de résultats particulièrement bons avec une SEQ assez imposante de 5,1118. Cela met en évidence au moins deux problèmes potentiels avec des modèles linéaires comme la régression : (1) ils peuvent être « surajustés » et (2) ils ne peuvent pas saisir les relations non linéaires entre les intrants et les extrants. Le terme « surajusté » désigne un modèle qui peut être si « peaufiné » par rapport à l’ensemble de données de formation qu’il donne de mauvais résultats dans l’ensemble d’essai. Certains diraient que le modèle a « appris le bruit » inhérent aux données de formation.

Amélioration non linéaire

L’optimisation précédente a permis de trouver des facteurs de pondération, {wi} qui produisaient la plus petite SEQ possible. Le modèle « f » a pris comme intrant les variables explicatives pour un certain point de données et son produit était une combinaison linéaire, comme le montre le tableau IV.

Tableau IV
Représentation visuelle du modèle linéaire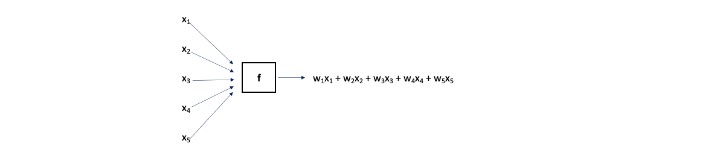

Les facteurs de pondération peuvent être choisis au hasard ou égalisés pour commencer l’optimisation. Pour chaque point de données de l’ensemble de formation, (x₁, x₂, x₃, x₄, x₅), la cote de risque modélisée, soit w₁x₁ + w₂x₂ + w₃x₃ + w₄x₄ + w₅x₅, est comparée à sa cote de risque réelle pour déterminer l’erreur. La SEQ (pour tous les points de données de l’ensemble de formation) est déterminée. L’optimisation ajuste ensuite les facteurs de pondération et calcule de nouveau la SEQ (améliorée). Cela se poursuit jusqu’à ce que les facteurs de pondération produisant la plus petite SEQ possible soient déterminés.

Comme nous l’avons mentionné, un tel modèle ne peut saisir les relations non linéaires entre les {x_i} d’une société et la cote de risque réelle de la société. Examinons une approche différente où nous considérons la combinaison linéaire comme un intrant d’une nouvelle fonction non linéaire A.

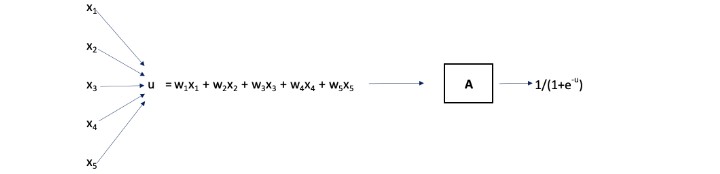
La fonction A prend comme intrant u= f(x₁, x₂, x₃, x₄, x₅), et son extrant est défini comme 1/(1+e^-u). Autrement dit, A est la fonction logistique.

Tableau V
Intégration d’un élément non linéaire au modèle

Les facteurs de pondération optimaux {w_i} restent à être déterminés et, encore une fois, nous minimisons la SEQ. Veuillez noter que ce qui précède est simplement une représentation visuelle de la composition des fonctions : A(f(x₁, x₂, x₃, x₄, x₅)). 

La fonction A joue un rôle important dans la création de la non linéarité dans le diagramme ci-dessus et elle est souvent appelée « nœud ». Le nœud prend une combinaison linéaire comme intrant et applique à cette valeur une fonction non linéaire, habituellement appelée « fonction d’activation ». Dans notre cas, l’intrant dans le nœud A est u= w₁x₁ + w₂x₂ + w₃x₃+ w₄x₄+ w₅x₅ et l’extrant est 1/(1+e^-u). La cote de risque prédite est cet extrant du nœud A. En pratique, un terme constant appelé « biais » est souvent utilisé dans la fonction d’activation. Par exemple, l’extrant du nœud pourrait être 1/(1+e^-u) +0,08, mais nous avons supposé que le biais est nul dans notre exemple. De nombreuses autres fonctions d’activation sont courantes, y compris la tangente hyperbolique et l’unité linéaire rectifiée (ndlt : rectified linear unit « ReLU ») qui est simplement R(t) = max(0,t).

Les {w_i} optimaux sont déterminés et nous avons maintenant un modèle où l’intrant correspond aux données d’une société comme (x₁, x₂, x₃, x₄, x₅) et l’extrant, c’est-à-dire la cote de risque prévue, est 1/(1+e^-u), où u = 1.3892x₁ + 3.3936 x₂ -7.0441 x₃ -0.9820 x₄ + 1.8822 x₅.

Ce modèle amélioré, non linéaire, présente une SEQ sur l’ensemble de formation de 0,0123, meilleure que la valeur de 0,1004 de l’approche linéaire. De plus, nous sommes passés de 5,1118 à 2,4084 dans la SEQ pour les données d’essai. Par souci de concision, les résultats numériques granulaires ne sont pas présentés ici, mais dans notre optimisation finale, nous examinerons plus en détail la performance du modèle.

Un réseau neuronal artificiel à deux couches

Comme dernière approche du problème, nous utilisons maintenant un RNA un peu plus compliqué pour illustrer la structure des nœuds, les fonctions d’activation et le concept d’apprentissage profond des couches.

Le tableau IV montre que notre nouveau RNA comporte maintenant les éléments suivants :

1. Cinq facteurs de pondération qui seront utilisés dans le nœud 1 et cinq autres facteurs de pondération qui sont utilisés pour le nœud 2.
2. Fonctions d’activation pour les nœuds 1 et 2 qui sont toutes les deux des fonctions logistiques (encore une fois).
3. Deux facteurs de pondération supplémentaires utilisés pour former une combinaison linéaire des extrants des nœuds 1 et 2.
4. Un troisième nœud, le nœud 3, prend la combinaison linéaire de (3) à titre d’intrant.
5. L’extrant du nœud 3, après une fonction logistique appliquée à son intrant, est la cote de risque modélisée.

Tableau VI
Représentation du réseau neuronal artificiel

Veuillez noter qu’il s’agit toujours d’une composition de fonctions où l’intrant est (x₁, x₂, x₃, x₄, x₅) et l’extrant (résultant de la composition des fonctions) est 1/(1+e^-z).

Comme auparavant, nous optimisons les facteurs de pondération (maintenant un total de 12 facteurs de pondération composés de {w_i}, {v_j}, and the {r_k} ) afin de minimiser la SEQ sur les données de formation. Les deux nœuds 1 et 2 forment ce que nous appelons la première « couche cachée » du RNA et le nœud 3 forme la deuxième couche cachée. Ces couches cachées se situent entre les intrants et les extrants du processus. Nous examinons maintenant la performance de cette optimisation sur les données de formation et d’essai.

Tableau VII
Performance du RNA au titre des données de formation

Tableau VIII
Performance du RNA au titre des données d’essai

Le RNA donne clairement de meilleurs résultats pour l’ensemble de données d’essai, tout en ajustant bien les données de formation. C’est exactement le type de résultat que nous recherchons dans des applications concrètes : l’objectif principal est la modélisation prédictive et l’ensemble de données d’essai est le terrain d’essai. La SEQ, qui est très proche de zéro, pointe vers le succès du modèle sur les données d’essai. Il convient de souligner que même si les erreurs quadratiques semblent être nulles, cela est attribuable à l’arrondissement, et elles sont en fait non nulles.

Il existe évidemment un large éventail de choix pour le nombre de nœuds, le nombre de facteurs de pondération, le choix des fonctions d’activation et le nombre de couches cachées dans le RNA.

Raison du bon fonctionnement de l’optimisation

Nous savons par expérience que la régression linéaire est populaire, en partie parce que sa solution peut être suivie de façon mathématique. Il est toujours facile d’obtenir les coefficients de régression. Certaines personnes qui ont tenté diverses optimisations dans un contexte d’affaires, peut-être en utilisant Excel, ont probablement remarqué que souvent, elles ne fonctionnent pas bien. La procédure d’optimisation a tendance à demeurer « coincée » dans un minimum local, qui n’est que le minimum de voisinage, plutôt que le minimum global que nous visons.

Comme mentionné, nous avons utilisé la méthode de descente de gradient dans nos optimisations. Il est important de voir que les extrants des diagrammes précédents sont des fonctions différentiables des valeurs d’extrant. Par conséquent, il existe des dérivées partielles de la SEQ pour chacun des facteurs de pondération. Il s’agit d’une condition qui rend la descente de gradient extrêmement puissante, surtout lorsque de nombreuses variables d’intrant sont envisagées.

De plus, nous n’avons pas imposé de contraintes aux facteurs de pondération, comme des limites inférieures ou des conditions arithmétiques sur leurs sommes ou leurs différences. Ce manque de contraintes et la différentiabilité font de la descente de gradient un outil efficace. Il est important de comprendre que nous pouvons encore être coincés dans un minimum local et ne pas produire une réponse optimale. Nous avons découvert que lorsqu’il y a un nombre « élevé » de dimensions dans le problème (c.-à-d. un nombre élevé de variables d’intrant), il est fréquent que le problème du minimum local disparaisse. Bien que les raisons sous-jacentes ne soient pas entièrement comprises, il s’agit certainement d’un résultat « heureux » et d’une raison fondamentale pour laquelle ces réseaux neuronaux ont connu un tel succès.

Bien entendu, l’optimisation de la descente de gradient peut entraîner divers problèmes, y compris ce qu’on appelle le problème de dissipation du gradient (ndlt : vanishing gradient). À chaque itération de la descente de gradient, chaque facteur de pondération reçoit un ajustement fondé sur la dérivée partielle de la SEQ (ou une autre fonction d’erreur ou pénalité) par rapport aux facteurs de pondération. Dans certains cas, les dérivées partielles pour un ou plusieurs facteurs de pondération commencent à s’approcher de zéro avant d’atteindre une solution optimale, ce qui empêche effectivement les facteurs de pondération de changer de valeur. Le RNA n’est alors pas en mesure d’« apprendre », c’est-à-dire que les progrès vers un ensemble optimal de facteurs de pondération cessent. Il existe toutefois un grand nombre de techniques pour atténuer ce problème.

Apprentissage profond en gestion des risques

Au tableau VI, nous avons deux couches cachées de nœuds entre l’intrant et l’extrant (final). Dans les applications compliquées comme la reconnaissance des images, la meilleure solution comporte souvent plusieurs couches. Lorsque le nombre de couches est élevé (p. ex., 5 à 7), on dit que le RNA est un réseau d’« apprentissage profond ». Ainsi, le terme « profond » dans l’apprentissage profond désigne un grand nombre de couches cachées.

Dans de nombreux cas, l’ajout de couches cachées dans un RNA n’améliore pas de façon significative la performance du modèle, mais dans de nombreuses applications complexes, cela s’avère utile.

Les applications de l’apprentissage profond ont connu d’énormes succès dans des domaines comme la reconnaissance vocale, les jeux de Go et d’échecs et le diagnostic médical. Les possibilités abondent également dans le domaine de la gestion du risque.

La gestion du risque porte souvent sur l’attribution d’une cote de risque à quelque chose en fonction de plusieurs variables explicatives connues. Lorsque la relation sous-jacente est à la fois numérique et compliquée, l’apprentissage profond peut représenter la solution.

Il conviendrait d’envisager l’attribution d’une catégorie de risque de souscription aux demandeurs d’assurance maladie. Nous pourrions prendre en considération des variables explicatives, notamment le statut de fumeur, l’état de santé déterminé par un médecin, l’âge, le sexe et d’autres indicateurs qui sont associés à la tendance des demandes de règlement futures. Comme il s’agit d’une relation complexe, il peut être utile de présenter le problème comme une optimisation de l’apprentissage profond.

Un autre exemple se trouve dans la gestion des risques liés aux tiers. Nous pourrions nous intéresser à l’estimation de la probabilité d’une atteinte à la sécurité des données chez un tiers. Cela peut être considéré comme une fonction de la cote de cybersécurité d’une société (fournie par l’une des nombreuses plateformes spécialisées à l’heure actuelle), du type de données qu’elle touche, du temps écoulé depuis sa dernière atteinte et d’autres variables explicatives. Ces données peuvent être utilisées, au moyen de l’apprentissage profond, pour attribuer une cote qui estime le risque d’atteinte, en tenant compte à la fois de la probabilité et de l’impact monétaire potentiel.

Le principal intrant humain dans les RNA est l’articulation des variables explicatives qui influencent la mesure inconnue de l’intérêt. Il est clair que les RNA connaîtront des succès encore plus impressionnants. Il est toutefois plus difficile de prédire quels seront les prochains domaines visés.

Les faits énoncés et les opinions formulées dans le présent document sont ceux de chaque auteur et ne correspondent pas nécessairement à ceux de la Society of Actuaries, des rédacteurs du magazine ou des employeurs des auteurs respectifs.

---

Damon Levine, CFA, ARM, CRCMP est expert-conseil en matière de risques, spécialisé dans les domaines bancaire et de la gestion du risque des sociétés d’assurance. On peut le joindre à DamonLevineCFA@gmail.com.