Conservation of Mortality and Assumption Integrity
By Tyler Armstrong, Randy Beams, and Robert Eaton
Product Matters!, November 2021

Introduction
Conservation of mortality, also known as “preservation of deaths” or “conservation of total deaths,” is the modeling principle an actuary may use to ensure consistency between assumptions of the total mortality of a population, and the assumptions of mortality among population subsets. This principle is an important consideration to maintaining assumption integrity.
The Concept
Conservation of mortality (“Conservation”), for the purpose of this article, means ensuring that the sum of the mortality assumption subsets of the population “sum” back to the overall population mortality assumptions. Assumption segments may be defined by age, gender, underwriting status, etc. For example, let QT denote the total mortality for a population, and let ![]() denote the total lives inforce in that population at time n. Also, let Qtx and
denote the total lives inforce in that population at time n. Also, let Qtx and ![]() represent the mortality and lives inforce respectively for each subset (x) of mortality. As an example, these subsets may represent preferred risks (x = 1) and standard risks (x = 2). Under the Conservation principle, the following formula will hold.
represent the mortality and lives inforce respectively for each subset (x) of mortality. As an example, these subsets may represent preferred risks (x = 1) and standard risks (x = 2). Under the Conservation principle, the following formula will hold.
An actuary may find it useful to apply Conservation in several cases, such as:
- When modeling mortality for preferred classes explicitly, as described in the valuation manual (VM-20).
- When assumed mortality is modified corresponding to a modeled shift in population, such as in estimating post-level term shock lapses for term life insurance.
- When the health status of an insured implies a change in assumed mortality, such as when modeling waiver of premium, long-term care (LTC), critical illness, or terminal illness benefits.
We explain each of these in the next section.
The Application
The principle of Conservation is particularly useful in the following applications.
Setting Mortality Assumptions across Life Insurance Preferred Risk Classes
In developing mortality assumptions across preferred risk classes, especially with the increased number of risk classes used today, companies often find that only some risk classes have sufficient credibility. Conservation may be used to help set mortality assumptions across all risk classes such that the expected aggregate company mortality assumption is more likely to be achieved. Another way to look at this is to use the aggregate company experience to determine the mortality for the individual risk classes. This ensures that when mortality segments are weighted together, the total expected mortality is not less (or more) than aggregate company experience. This approach is spelled out as one option in VM-20.[1]
Use techniques to further subdivide the aggregate experience into the various mortality segments (e.g., start with aggregate nonsmoker and then use the conservation of total deaths principle, normalization or other approach to divide the aggregate mortality into super preferred, preferred and residual standard non-smoker class assumptions).
Post-Level Premium Term Mortality
Shock lapses occur in products with dramatic increases in premiums or charges, such as following the level-premium period in level term life products. Healthier policyholders tend to lapse their policies at higher rates, because they can typically find lower premium rates elsewhere. The mortality of the residual population after this “selective” lapsation is commonly estimated using the Dukes/MacDonald[2] method, which applies the Conservation principle.
Hybrid Life + LTC Products
Hybrid products (also referred to as combination, or “combo” products) are life insurance or annuity contracts with LTC related benefits. When an insured with this type of contract becomes eligible for an LTC claim, modelers refer to them as a “disabled life.” When modeling hybrid products, actuaries typically assume that disabled lives have higher mortality than the mortality assumed in aggregate for the base life contract. With an estimate of total life and disabled life mortality, Conservation can be used to model the mortality of the remaining active life population. Similarly, if the actuary has estimates of total mortality and active life mortality, Conservation can be used to solve for the mortality of the disabled lives.
Critical and Terminal Illness Riders
Actuaries often model increased mortality for life insurance policyholders who have a critical illness or terminal illness rider and who make a claim for critical or terminal illness rider benefits. Similar to the disabled lives pool in the hybrid products (above), the actuary can use claim status as an indicator of future mortality. The complement to the disabled lives pool is a pool of the remaining healthy (or ‘active’) lives. The company can derive the healthy life population mortality with a known disabled life mortality, using the Conservation principle. A detailed discussion of pricing these various morbidity acceleration benefits can be found in the June 2021 edition of Product Matters![3]
Special Note on Conservation for Acceleration-Only Riders
Most critical illness, terminal illness, and chronic illness riders to life insurance policies accelerate the death benefit of the underlying life insurance contract when the insured experiences certain health events. Some LTC hybrid products feature acceleration-only riders as well, i.e., they do not include LTC benefits that extend beyond the amount of the base policy death benefits.
For these acceleration-only riders, applying the Conservation principle requires tracking the lives of disabled policyholders after they have exhausted their contractual benefits. As an example, imagine a policyholder who purchases a whole life contract with an LTC acceleration-only rider, where the acceleration benefit allows the policyholder to receive 4 percent of the death benefit each month once they trigger LTC benefits. Some policyholders who receive these benefits may survive for more than 25 months, after which point they will have exhausted their death benefits and their contract may terminate. This policyholder is still alive and would have different mortality than a policyholder who had died within the acceleration period. As mortality beyond the acceleration period is not typically tracked, the Conservation principle would be difficult to apply, as accurate mortality for the disabled life population is typically not available with the acceleration benefit.
Thus, to apply the Conservation principle appropriately to life policies with acceleration-only riders, the actuary will want to track the lives of disabled insureds in the models even after they have exhausted their contractual benefits. This may be negligible in the case of policyholders with a terminal illness (who are expected to have very few months left to live). The impact can be substantial for policies with critical illness benefits, where people may live decades following a heart attack, or for LTC policies where younger insureds may live for many years after the onset of dementia.
Disability Waiver of Premium Riders
Disability insurance is often sold with an accompanying waiver of premium rider. Once disabled, the rider benefit covers the insured’s premium payments. The population on waiver status may be modeled with a segment-specific mortality. The Conservation principle may be used to develop the appropriate mortality for the residual, healthy population.
The Art
While the principle of Conservation of mortality is expressed as a mathematical equation, applying this principle is not always straightforward. In some cases, the Conservation principle can yield unreasonable or unintuitive results, adding to model complexity. In addition, ongoing monitoring and assumption refinement may require more granular data collection. The remainder of this article will focus on resolving potential discrepancies in modeled results.
The actuary may see unusual or unexpected results arise if they use different sources of data or claims experience to develop the mortality assumptions of the total population, compared with those of subsets of that population. This is often the case when actuaries develop assumptions for hybrid life and LTC products. The actuary will rely on industry data for disabled mortality, due to the lack of credible internal experience.
Two examples are given below.
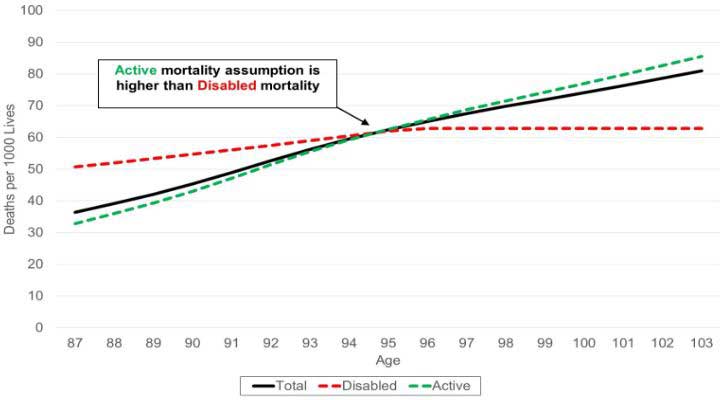
Figure 1 illustrates a possible situation where the disabled life mortality assumption drops below the total mortality assumption at older ages. This results in the unintended consequence of a higher active than disabled mortality using Conservation.
Figure 1
Mortality Comparison Disabled Mortality Falls below Active
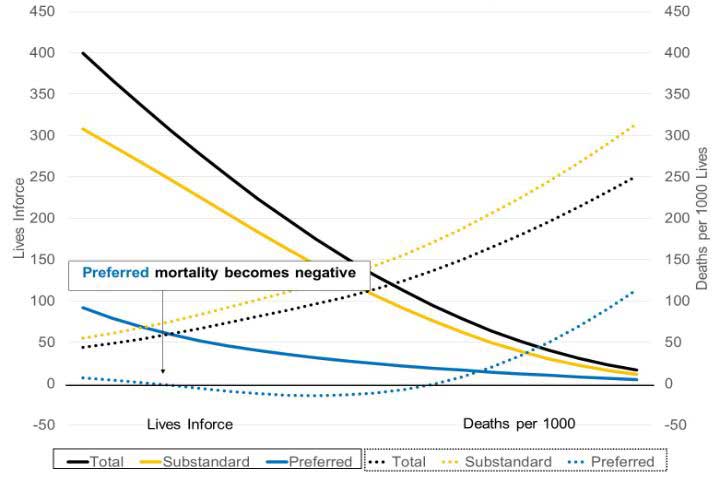
Similarly, if a company projects another decrement at segment-varying rates (e.g., different lapse rates by risk class) it becomes possible to have the weighted aggregate mortality become greater than assumed total mortality. For example, it is common for companies to assume lower lapses for the preferred class and higher for the substandard class. Figure 2 illustrates an example where preferred lives run off more quickly than substandard lives due to differing lapse rates. This leads to negative mortality rates under Conservation for the preferred class in later years due to the small proportion of preferred lives to total lives.
Figure 2
Lives and Mortality Projections Solving for Preferred Lives Mortality
It is an artform using actuarial judgement to determine the appropriate method to handle discrepancies or unreasonable results. Below are several approaches to address these situations, including some potential drawbacks of each. The approaches include:
- Segment corridors
- Adjustment of mortality assumptions
- Negative lives
Segment Corridors
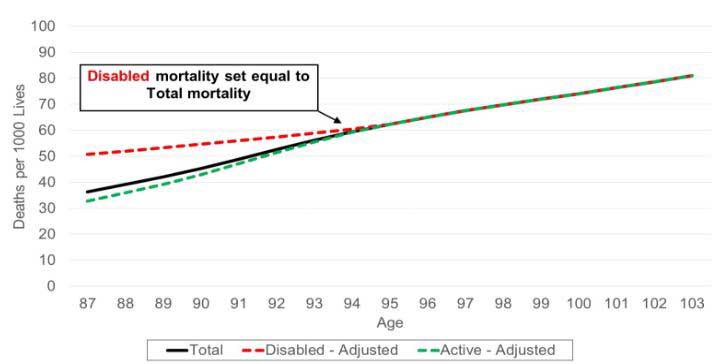
Corridors, or caps and floors, may be used to preserve reasonableness. Assume we have defined total life and disabled life mortalities and wish to use Conservation to derive our active life mortality. Also assume as in Figure 1, the disabled life mortality drops below total life mortality at older ages. To prevent this unintuitive relationship, we place a floor on the disabled life mortality equal to total life mortality as demonstrated in Figure 3.
Figure 3
Mortality Comparison Floored Disabled Mortality
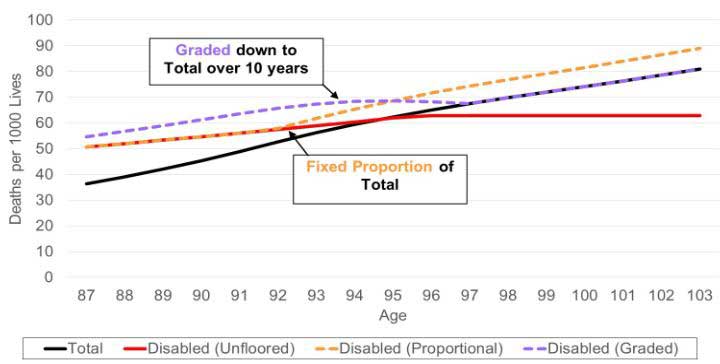
The actuary should use judgement in setting appropriate corridors and is not limited to a floor or cap equal to total life mortality. In some cases, a fixed proportion (such as 110 percent of total mortality) or a corridor that starts with a high proportion and grades to a lower, fixed proportion of total life mortality at older ages may be more appropriate. Figure 4 illustrates each case.
Figure 4
Mortality Comparison Graded Disabled Mortality
Segment corridors are a popular option due to their simplicity, intuitive nature, and ease of implementation. The main drawback to the corridor approach is a potential lack of refinement and over-correction for subsets of the population. For instance, if the actuary uses the corridor approach, then disabled life mortality may be forced too high, and subsequently active life mortality too low. This may lead to understatement of reserves or other inaccuracies.
Adjust Mortality Assumptions
The actuary may adjust the total or segment(s) mortality, such that Conservation is more likely to hold. When determining which mortality assumption(s) to adjust, the actuary should consider several factors:
- Credibility of assumptions
- Product risk profile
- Projection type (pricing, valuation, cash flow testing, etc.) and materiality
- Relevance of experience (e.g., a company has a new underwriting process)
Segment mortality is usually not as credible as total population mortality or is derived from industry experience as opposed to company experience. This is often the case when the company is bringing a new product or benefit to market. In these situations, the actuary should consider adjusting industry derived assumptions to align more closely with the company’s own.
A second consideration should be the product’s risk profile. For example, with a term product in the post-level period, an increase in assumed mortality for the persisting population will increase projected benefits and thus is more realistic. The actuary should consider the appropriate level of conservatism when determining which assumptions to adjust and by how much.
Lastly, the actuary should consider the purpose of the projection and materiality of Conservation discrepancies. In a valuation projection, results in later years (i.e., in the tail) are often more important than similar points in initial pricing projections. For pricing projections where discrepancies occur decades from issue, the actuary may elect to maintain current assumptions, i.e., make no adjustments as it has little to no effect on premium rates. However, for valuation runs, especially in later policy years where reserves and benefits become elevated and more material on a present value basis, accuracy in the tail becomes increasingly important to the company and regulators. The actuary should take increased care in adjusting assumptions in this latter case.
Note that multiple iterations may be needed to fine tune assumptions. Adjusting mortality assumptions is advantageous to the actuary as it takes a more nuanced approach: this approach allows for fine-tuning the assumption over time at increased granularity, likely allowing more accurate assumptions to be utilized. However, this approach is often more complicated than a simple corridor, may require more work, and requires more documentation and justification than the other approaches.
Negative Lives
Perhaps the simplest solution is to allow for projected lives to become negative in the residual population. This method places the importance onto the defined segment mortality as opposed to the total life mortality. In other words, the defined segment mortality remains unadjusted, while the negative lives in the residual population allows the Conservation formula to hold together, if only in theory. These lives often “resurrect” by the end of the projection when the lives for all segments are zero.
Though simple, assuming negative lives is often not the best solution. This approach replaces one or more discontinuity with another and may be inappropriate for pricing, valuation exercises such as VM-20 calculations, or cash flow testing.
The actuary should consider and test each option depending on their desired use case, risk profile, and product design. Each situation presents its own unique characteristics to consider and as such this step is more of an art form than a science.
Conclusion
Conservation of mortality is an important principle for actuaries to consider when modeling multiple mortality assumptions in concert. If an actuary is unable to set appropriate mortality assumptions for each segment with credible experience, using a Conservation is important (if not required) to avoid counterintuitive pricing conclusions, regulatory violations, understatement of future reserves, or other confusions.
Statements of fact and opinions expressed herein are those of the individual authors and are not necessarily those of the Society of Actuaries, the newsletter editors, or the respective authors’ employers.
Tyler Armstrong, FSA, is an actuary at Milliman. He can be reached at tyler.armstrong@milliman.com.
Randy Beams, FSA, is an actuary at Milliman. He can be reached at randy.beams@milliman.com.
Robert Eaton, FSA, MAAA is a principal at Milliman. He can be reached at robert.eaton@milliman.com.